
如圖,△ABC中,AB=AC,AD,CD分別是△ABC兩個外角的平分線。
(1)求證:AC=AD;
(2)若∠B=60°,求證:四邊形ABCD是菱形.
(1)根據三角形外角的性質得到∠CAF=∠B+∠ACB,由AB=AC可得∠B=∠ACB,即可得到∠CAF=2∠B,根據角平分線的性質可得∠CAF=2∠FAD,即可得到∠B=∠FAD,則可得AD//BC,根據平行線的性質可得∠D=∠DCE,再根據角平分線的性質可得∠DCE=∠ACD,即可證得結論;
(2)由△ABC中,AB=AC,∠B=60°可證得△ABC是等邊三角形,即得AB=BC=AC,由AD=AC可得AD=BC,再結合AD//BC可證得四邊形ABCD是平行四邊形,再有AB=BC即可證得結論.
解析試題分析:(1)∵∠CAF是△ABC的外角
∴∠CAF=∠B+∠ACB
∵AB=AC
∴∠B=∠ACB
∴∠CAF=2∠B
∵AD是△ABC兩個外角的平分線
∴∠CAF=2∠FAD
∴∠B=∠FAD
∴AD//BC
∴∠D=∠DCE
∵CD是△ABC外角的平分線
∴∠DCE=∠ACD
∴AC=AD;
(2)∵△ABC中,AB=AC,∠B=60°
∴△ABC是等邊三角形
∴AB=BC=AC
∵AD=AC
∴AD=BC
又∵AD//BC
∴四邊形ABCD是平行四邊形
∵AB=BC
∴四邊形ABCD是菱形.
考點:三角形的外角的性質,角平分線的性質,平行四邊形的判定和性質,菱形的判定
點評:此類問題是初中數學的重點,是中考常見題,一般難度不大,需熟練掌握.


科目:初中數學 來源:北師大版(新課標) 九年級(下) 題型:
| |||||
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:如圖,把長方形紙片ABCD沿EF折疊后.點D與點B重合,點C落在點C′的位置上.若∠1=60°,AE=1.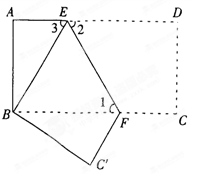
(1)求∠2、∠3的度數;
(2)求長方形紙片ABCD的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,AB是半圓O的直徑,AD為弦,BC是半圓O的切線,OC∥AD,
【小題1】求證:CD是半圓O的切線
【小題2】若BD=BC=6,求AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com