
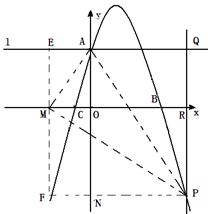
已知拋物線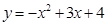 交y軸于點A,交x軸于點B,C(點B在點C的右側(cè))。如圖,過點A作垂直于y軸的直線l. 在y軸右側(cè)、位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q,交x軸于R,連接AP.
交y軸于點A,交x軸于點B,C(點B在點C的右側(cè))。如圖,過點A作垂直于y軸的直線l. 在y軸右側(cè)、位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q,交x軸于R,連接AP.
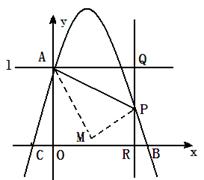
(1)求A,B,C三點的坐標(biāo);
(2)如果以A,P,Q三點構(gòu)成的三角形與△AOC相似,求出點P的坐標(biāo);
(3)若將△APQ沿AP對折,點Q的對應(yīng)點為點M. 是否存在點P,使得點M落在x軸上.若存在,求出點P的坐標(biāo);若不存在,請說明理由.
(1)A(0,4),B(4,0),C(-1,0);(2)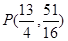 ,
,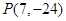 ;(3)
;(3)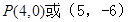
【解析】
試題分析:(1)分別求得拋物線 與坐標(biāo)軸的交點坐標(biāo)即可得到結(jié)果;
與坐標(biāo)軸的交點坐標(biāo)即可得到結(jié)果;
(2)設(shè)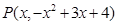 ,則
,則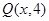 ,
,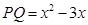 ,分
,分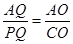 與
與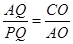 兩種情況分析即可得到結(jié)果;
兩種情況分析即可得到結(jié)果;
(3)構(gòu)造正方形PQEF,ME=OA=4,AM=AQ=x,則PM=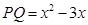 ,證得
,證得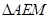 ~
~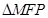 ,根據(jù)相似三角形的性質(zhì)可表示出PF,從而可以表示出CM,在
,根據(jù)相似三角形的性質(zhì)可表示出PF,從而可以表示出CM,在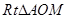 中,根據(jù)勾股定理即可列方程求得結(jié)果.
中,根據(jù)勾股定理即可列方程求得結(jié)果.
(1)在 中,
中,
當(dāng)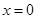 時,
時,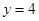 ;
;
當(dāng)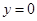 時,
時, ,解得
,解得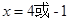
∴A(0,4),B(4,0),C(-1,0);
(2)設(shè)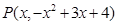 ,則
,則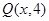 ,
,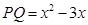
當(dāng)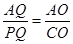 時,得
時,得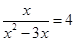 ,解得
,解得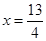
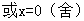 ,此時
,此時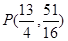
當(dāng)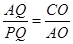 時,得
時,得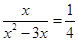 ,解得
,解得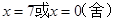 ,此時
,此時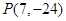 ;
;
(3)如圖構(gòu)造正方形PQEF,ME=OA=4,AM=AQ=x
PM=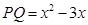 ,
,
證得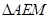 ~
~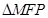
有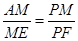 ,即
,即 ,解得
,解得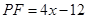
∴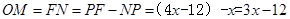
在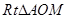 中,
中,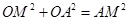
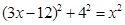
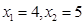
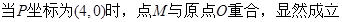
∴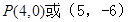 .
.
考點:二次函數(shù)的綜合題
點評:本題知識點多,綜合性強,難度較大,一般是中考壓軸題,主要考查學(xué)生對二次函數(shù)的熟練掌握情況.


科目:初中數(shù)學(xué) 來源: 題型:
 AB=5OB,設(shè)點E(x,y)是拋物線上一動點,且位于第四象限,四邊形OEAF是以O(shè)A為對角線的平行四邊形.
AB=5OB,設(shè)點E(x,y)是拋物線上一動點,且位于第四象限,四邊形OEAF是以O(shè)A為對角線的平行四邊形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
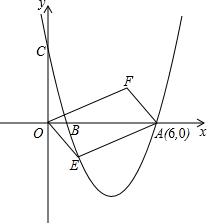 AB=5OB,設(shè)點E(x,y)是拋物線上一動點,且位于第四象限,四邊形OEAF是以O(shè)A為對角線的平行四邊形.
AB=5OB,設(shè)點E(x,y)是拋物線上一動點,且位于第四象限,四邊形OEAF是以O(shè)A為對角線的平行四邊形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012屆浙江省杭州市上城區(qū)中考二模數(shù)學(xué)試卷(帶解析) 題型:解答題
已知拋物線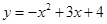 交y軸于點A,交x軸于點B,C(點B在點C的右側(cè)).過點A作垂直于y軸的直線l. 在位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q.連接AP.
交y軸于點A,交x軸于點B,C(點B在點C的右側(cè)).過點A作垂直于y軸的直線l. 在位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q.連接AP.
(1)寫出A,B,C三點的坐標(biāo);
(2)若點P位于拋物線的對稱軸的右側(cè):
①如果以A,P,Q三點構(gòu)成的三角形與△AOC相似,求出點P的坐標(biāo);
②若將△APQ沿AP對折,點Q的對應(yīng)點為點M.是否存在點P,使得點M落在x軸上.若存在,求出點P的坐標(biāo);若不存在,請說明理由.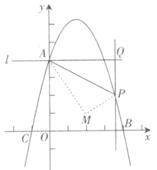
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省杭州市上城區(qū)中考二模數(shù)學(xué)試卷(解析版) 題型:解答題
已知拋物線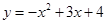 交y軸于點A,交x軸于點B,C(點B在點C的右側(cè)).過點A作垂直于y軸的直線l. 在位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q.連接AP.
交y軸于點A,交x軸于點B,C(點B在點C的右側(cè)).過點A作垂直于y軸的直線l. 在位于直線l下方的拋物線上任取一點P,過點P作直線PQ平行于y軸交直線l于點Q.連接AP.
(1)寫出A,B,C三點的坐標(biāo);
(2)若點P位于拋物線的對稱軸的右側(cè):
①如果以A,P,Q三點構(gòu)成的三角形與△AOC相似,求出點P的坐標(biāo);
②若將△APQ沿AP對折,點Q的對應(yīng)點為點M.是否存在點P,使得點M落在x軸上.若存在,求出點P的坐標(biāo);若不存在,請說明理由.
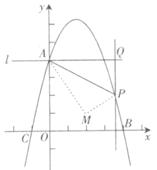
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com