
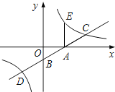
【題目】如圖,直線![]() 與
與![]() ,
,![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,與反比例函數
,與反比例函數![]() 圖象交于點
圖象交于點![]() ,
,![]() ,過點
,過點![]() 作
作![]() 軸的垂線交該反比例函數圖象于點
軸的垂線交該反比例函數圖象于點![]() .
.
![]() 求點
求點![]() 的坐標.
的坐標.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②試判斷點![]() 與點
與點![]() 是否關于原點
是否關于原點![]() 成中心對稱?并說明理由.
成中心對稱?并說明理由.
【答案】![]() 點
點![]() 的坐標為
的坐標為![]() ;②點
;②點![]() 與點
與點![]() 關于原點
關于原點![]() 成中心對稱.理由見解析.
成中心對稱.理由見解析.
【解析】
(1)令一次函數中y=0,解關于x的一元一次方程,即可得出結論;
(2)①過點C作CF⊥x軸于點F,設AE=AC=t,由此表示出點E的坐標,利用特殊角的三角形函數值,通過計算可得出點C的坐標,再根據反比例函數圖象上點的坐標特征可得出關于t的一元二次方程,解方程即可得出結論;
②根據點在直線上設出點D的坐標,根據反比例函數圖象上點的坐標特征可得出關于點D橫坐標的一元二次方程,解方程即可得出點D的坐標,結合①中點E的坐標即可得出結論.
![]() 當
當![]() 時,得
時,得![]() ,解得:
,解得:![]() .
.
∴點![]() 的坐標為
的坐標為![]() .:
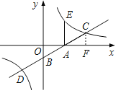
.:![]() ①過點
①過點![]() 作
作![]() 軸于點
軸于點![]() ,如圖所示.
,如圖所示.
設![]() ,點
,點![]() 的坐標是
的坐標是![]() ,
,
B(0,![]() )∴AB=3
)∴AB=3
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴點![]() 的坐標是
的坐標是![]() .
.
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]() .
.
②點![]() 與點
與點![]() 關于原點
關于原點![]() 成中心對稱,理由如下:
成中心對稱,理由如下:
設點![]() 的坐標是
的坐標是![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴點![]() 的坐標是
的坐標是![]() .
.
又∵點![]() 的坐標為
的坐標為![]() ,
,
∴點![]() 與點
與點![]() 關于原點
關于原點![]() 成中心對稱.
成中心對稱.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩家園林公司承接了某項園林綠化工程,己知乙公司單獨完成此項工程所需要的天數是甲公司單獨完成所需要天數的1.5倍,如果甲公司先單獨工作10天,再由乙公司單獨工作l5天,這樣恰好完成整個工程的![]() ;
;
(1)求甲、乙兩公司單獨完成這項工程各需多少天?
(2)園林部門要求完成該綠化工程的時間不得超過30天,甲、乙公司合作若干天后,甲公司另有項目離開,剩下的工程由乙公司單獨完成,求甲、乙兩公司至少合作多少天.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展研學旅行活動,準備去的研學基地有A(曲阜)、B(梁山)、C(汶上),D(泗水),每位學生只能選去一個地方,王老師對本全體同學選取的研學基地情況進行調查統計,繪制了兩幅不完整的統計圖(如圖所示).
(1)求該班的總入數,并補全條形統計圖.
(2)求D(泗水)所在扇形的圓心角度數;
(3)該班班委4人中,1人選去曲阜,2人選去梁山,1人選去汶上,王老師要從這4人中隨機抽取2人了解他們對研學基地的看法,請你用列表或畫樹狀圖的方法,求所抽取的2人中恰好有1人選去曲阜,1人選去梁山的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校計劃在如圖所示的空地 ABCD 上種植草皮,經測量∠ADC=90°,CD = 6m ,AD = 8m , AB=26m , BC= 24m .

(1)求出空地 ABCD 的面積;
(2)若每種植 1 平方米草皮需要 200 元,問總共需投入多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
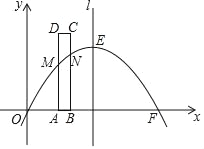
【題目】如圖,已知拋物線y=ax2+bx與x軸分別交于原點O和點F(10,0),與對稱軸l交于點E(5,5).矩形ABCD的邊AB在x軸正半軸上,且AB=1,邊AD,BC與拋物線分別交于點M,N.當矩形ABCD沿x軸正方向平移,點M,N位于對稱軸l的同側時,連接MN,此時,四邊形ABNM的面積記為S;點M,N位于對稱軸l的兩側時,連接EM,EN,此時五邊形ABNEM的面積記為S.將點A與點O重合的位置作為矩形ABCD平移的起點,設矩形ABCD平移的長度為t(0≤t≤5).
(1)求出這條拋物線的表達式;
(2)當t=0時,求S△OBN的值;
(3)當矩形ABCD沿著x軸的正方向平移時,求S關于t(0<t≤5)的函數表達式,并求出t為何值時,S有最大值,最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在半徑為4的⊙O中,CD為直徑,AB⊥CD且過半徑OD的中點,點E為⊙O上一動點,CF⊥AE于點F.當點E從點B出發順時針運動到點D時,點F所經過的路徑長為( )

A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本小題滿分7分) 已知:如圖,A是⊙O上一點,半徑OC的延長線與過點A的直線交于B點,OC=BC,AC=![]() OB.
OB.
(1)求證:AB是⊙O的切線;
(2)若∠ACD=45°,OC=2,求弦CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖所示,則abc,b2-4ac,2a+b,a+b+c這四個式子中,值為正數的有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
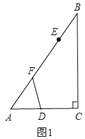
【題目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 由
由![]() 出發沿
出發沿![]() 向點
向點![]() 勻速運動,同時點
勻速運動,同時點![]() 由
由![]() 出發沿
出發沿![]() 向點
向點![]() 勻速運動,它們的速度相同,點
勻速運動,它們的速度相同,點![]() 在
在![]() 上,
上,![]() ,且點
,且點![]() 在點
在點![]() 的下方,當點
的下方,當點![]() 到達點
到達點![]() 時,點
時,點![]() ,
,![]() 也停止運動,連接
也停止運動,連接![]() ,設
,設![]() .解答下列問題:
.解答下列問題:
![]() 如圖
如圖![]() ,當
,當![]() 為何值時,
為何值時,![]() 為直角三角形;
為直角三角形;
![]() 如圖
如圖![]() ,把
,把![]() 沿
沿![]() 翻折,使點
翻折,使點![]() 落在
落在![]() 點.
點.
①當![]() 為何值時,四邊形
為何值時,四邊形![]() 為菱形?并求出菱形的面積;
為菱形?并求出菱形的面積;
②如圖![]() ,分別取
,分別取![]() ,
,![]() 的中點
的中點![]() ,
,![]() ,在整個運動過程中,則線段
,在整個運動過程中,則線段![]() 掃過的區域的形狀為________,其面積為________.
掃過的區域的形狀為________,其面積為________.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com