
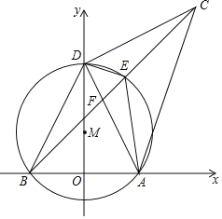
【題目】我們知道:有一內角為直角的三角形叫做直角三角形.類似地,我們定義:有一內角為45°的三角形叫做半直角三角形.如圖,在平面直角坐標系中,O為原點,A(4,0),B(﹣4,0),D是y軸上的一個動點,∠ADC=90°(A、D、C按順時針方向排列),BC與經過A、B、D三點的⊙M交于點E,DE平分∠ADC,連結AE,BD.顯然△DCE、△DEF、△DAE是半直角三角形.
(1)求證:△ABC是半直角三角形;
(2)求證:∠DEC=∠DEA;
(3)若點D的坐標為(0,8),求AE的長.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)先求得∠ADE=45°,由同弧所對的圓周角可知:∠ABE=∠ADE=45°,根據定義得:△ABC是半直角三角形;
(2)根據垂直平分線的性質得:AD=BD,由等角對等邊得:∠DAB=∠DBA,由D、B、A、E四點共圓,
則∠DBA+∠DEA=180°,可得結論;
(3)設⊙M的半徑為r,根據勾股定理列方程為:(8-r)2+42=r2,可得⊙M 的半徑為5,由同弧所對的圓心角和圓周角的關系可得∠EMA=2∠ABE=90°,根據勾股定理可得結論;
(1)∵∠ADC=90°,DE平分∠ADC,
∴∠ADE=45°,
∵∠ABE=∠ADE=45°,
∴△ABC是半直角三角形
(2)∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四點共圓,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC
(3)如圖1,連接AM,ME,

設⊙M的半徑為r,
∵點D的坐標為(0,8),
∴OM=8﹣r,
由OM2+OA2=MA2得:(8﹣r)2+42=r2,
解得r=5,
∴⊙M 的半徑為5
∵∠ABE=45°
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=52+52=50,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】某汽車4S店銷售某種型號的汽車,每輛進貨價為15萬元,該店經過一段時間的市場調研發現:當銷售價為25萬元時,平均每周能售出8輛,而當銷售價每降低0.5萬元時,平均每周能多售出1輛.該4S店要想平均每周的銷售利潤為90萬元,并且使成本盡可能的低,則每輛汽車的定價應為多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1995年聯合國教科文組織把每年4月23日確定為“世界讀書日”.某中學為了解全校1000名學生平均每天閱讀課外書報的時間,隨機調查了該校50名學生一周內平均每天閱讀課外書報的時間,結果如下表:
時間(分) | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
人 數 | 8 | 12 | 7 | 5 | 4 | 3 | 4 | 2 | 3 | 2 |
根據上述信息完成下列各題:
(1)在統計表(上表)中,眾數是 分,中位數是 分;
(2)估計該學校平均每天閱讀課外書報的時間不少于35分鐘的學生大約 人;
小明同學根據上述信息制作了如下頻數分布表和頻數分布直方圖,請你完成下列問題:
(3)頻數分布表中![]() ,
,![]() ;
;
(4)補全頻數分布直方圖.

查看答案和解析>>
科目:初中數學 來源: 題型:
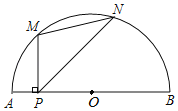
【題目】如圖,P是半圓O中![]() 所對弦AB上一動點,過點P作PM⊥AB交
所對弦AB上一動點,過點P作PM⊥AB交![]() 于點M,作射線PN交
于點M,作射線PN交![]() 于點N,使得∠NPB=45°,連接MN.已知AB=6cm,設A,P兩點間的距離為xcm,M,N兩點間的距離為ycm.(當點P與點A重合時,點M也與點A重合,當點P與點B重合時,y的值為0)
于點N,使得∠NPB=45°,連接MN.已知AB=6cm,設A,P兩點間的距離為xcm,M,N兩點間的距離為ycm.(當點P與點A重合時,點M也與點A重合,當點P與點B重合時,y的值為0)
小超根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小超的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,得到了y與x的幾組對應值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(說明:補全表格時相關數值保留一位小數)
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:當MN=2AP時,AP的長度約為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形的邊長都是1,每個小正方形的頂點叫做格點.△ABC的三個頂點A,B,C都在格點上.將△ABC繞點A按順時針方向旋轉90°得到△AB′C′.
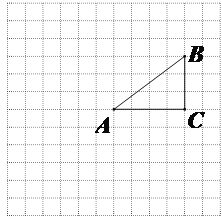
(1)在正方形網格中,畫出△AB′C′;
(2)計算線段AB在變換到AB′的過程中掃過的區域的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
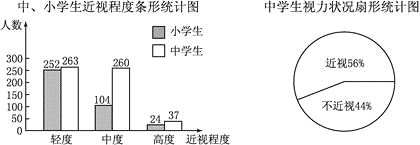
【題目】某市青少年健康研究中心隨機抽取了本市1000名小學生和若干名中學生,對他們的視力狀況進行了調查,并把調查結果繪制成如下統計圖.(近視程度分為輕度、中度、高度三種)
(1)求這1000名小學生患近視的百分比.
(2)求本次抽查的中學生人數.
(3)該市有中學生8萬人,小學生10萬人.分別估計該市的中學生與小學生患“中度近視”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于A(1,t+1),B(t-5,-1)兩點.
的圖象交于A(1,t+1),B(t-5,-1)兩點.
(1)求一次函數和反比例函數的解析式;
(2)若點(c,p)和(n,q)是反比例函數y=![]() 圖象上任意兩點,且滿足c=n+1時,求
圖象上任意兩點,且滿足c=n+1時,求![]() 的值.
的值.
(3)若點M(x1,y1)和N(x2,y2)在直線AB(不與A、B重合)上,過M、N兩點分別作y軸的平行線交雙曲線于E、F,已知x1<-3,0<x2<1,當x1x2=-3時,判斷四邊形NFEM的形狀.并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
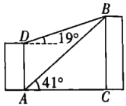
【題目】如圖,已知一居民樓![]() 前方
前方![]() 處有一建筑物
處有一建筑物![]() ,小敏在居民樓的頂部
,小敏在居民樓的頂部![]() 處和底部
處和底部![]() 處分別測得建筑物頂部
處分別測得建筑物頂部![]() 的仰角為
的仰角為![]() 和
和![]() ,求居民樓的高度
,求居民樓的高度![]() 和建筑物的高度
和建筑物的高度![]() (結果取整數).
(結果取整數).
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
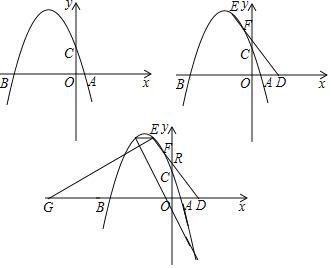
【題目】拋物線y=﹣![]() x+c交x軸于A、B兩點(B在A左側),交y軸于C,AB=10.
x+c交x軸于A、B兩點(B在A左側),交y軸于C,AB=10.
(1)求拋物線的解析式;
(2)在A點右側的x軸上取點D,E為拋物線上第二象限內的點,連接DE交拋物線另外一點F,tan∠BDE=![]() ,DF=2EF,求E點坐標;
,DF=2EF,求E點坐標;
(3)在(2)的條件下,點G在x軸負半軸上,連接EG,EH∥AB交拋物線另外一點H,點K在第四象限的拋物線上,設DE交y軸于R,∠EHK=∠EGD+∠ORD,當HK=EG,求K點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com