
【題目】如圖,AB是⊙O的直徑,C是弧![]() 的中點,⊙O的切線BD交AC的延長線于點D,E是OB的中點,CE的延長線交切線BD于點F,AF交⊙O于點H,連接BH.
的中點,⊙O的切線BD交AC的延長線于點D,E是OB的中點,CE的延長線交切線BD于點F,AF交⊙O于點H,連接BH.
⑴求證:AC=CD.
⑵若OB=2,求BH的長.

科目:初中數學 來源: 題型:
【題目】如圖,![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,連接
上,連接![]() ,
,![]() 、
、![]() 的平分線交于點
的平分線交于點![]() ,
,![]() 、
、![]() 的平分線交于點
的平分線交于點![]() .
.
![]() 求證:四邊形
求證:四邊形![]() 是矩形.
是矩形.
![]() 小明在完成
小明在完成![]() 的證明后繼續進行了探索,過點
的證明后繼續進行了探索,過點![]() 作
作![]() ,分別交
,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,過點
,過點![]() 作
作![]() ,分別交
,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,得到四邊形
,得到四邊形![]() .此時,他猜想四邊形
.此時,他猜想四邊形![]() 是菱形.請在下列框圖中補全他的證明思路.
是菱形.請在下列框圖中補全他的證明思路.
小明的證明思路:由![]() ,
,![]() ,
,![]() 易證,四邊形
易證,四邊形![]() 是平行四邊形.要證□
是平行四邊形.要證□![]() 是菱形,只要證
是菱形,只要證![]() .由已知條件________,
.由已知條件________,![]() ,可證
,可證![]() ,故只要證
,故只要證![]() ,即證
,即證![]() ,易證________,________,故只要證
,易證________,________,故只要證![]() ,易證
,易證![]() ,
,![]() ,________,故得
,________,故得![]() ,即可得證.
,即可得證.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰直角△ABC中,∠ACB=90°,P是線段BC上一動點(與點B、C不重合),連接AP,延長BC至點Q,使得CQ=CP,過點Q作QH⊥AP于點H,交AB于點M.
(1)當AP平分∠BAC時,試說明AM=AN.
(2)若∠PAC=m,求∠AMQ的大小(用含m的式子表示).
(3)用等式表示線段MB與PQ之間的數量關系,并證明.
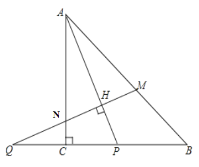
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形OABC的一邊OA在x軸上,將菱形OABC繞原點O順時針旋轉75°至OA’B’C’的位置.若OB=![]() ,∠C=120°,則點B’的坐標為( )
,∠C=120°,則點B’的坐標為( )
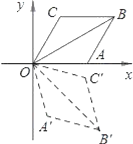
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,以原點O為圓心的圓過點A(5,0),直線y=kx-2k+3(k≠0)與⊙O交于B、C兩點,則弦BC的長的最小值為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() 的平分線
的平分線![]() 和
和![]() 的外角平分線
的外角平分線![]() 相交于點
相交于點![]() ,分別交
,分別交![]() 和
和![]() 的延長線于
的延長線于![]() ,
,![]() .過
.過![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;其中正確的結論有( )
;其中正確的結論有( )
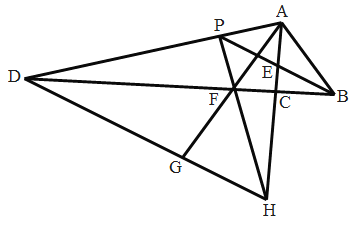
A.4個B.3個C.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,中心為點
,中心為點![]() ,現有邊長大小不確定的正方形
,現有邊長大小不確定的正方形![]() ,中心也為點
,中心也為點![]() ,可繞點
,可繞點![]() 任意旋轉,在旋轉過程中,正方形
任意旋轉,在旋轉過程中,正方形![]() 始終在正方形
始終在正方形![]() 內(包括正方形的邊),當正方形
內(包括正方形的邊),當正方形![]() 邊長最大時,
邊長最大時,![]() 的最小值為________.
的最小值為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com