
【題目】如圖,點B在線段AC上,點E在線段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分別是AE,CD的中點.
(1)求證:△ABM≌△DBN;
(2)試探索BM和BN的關系,并證明你的結論.

【答案】(1)見解析;(2)△MBN是等腰直角三角形,理由見解析
【解析】
(1)根據SAS即可證明結論;(2)通過證明△ABM≌△DBN可證明BM=BN,∠ABM=∠DBN.根據∠ABD=∠DBC,∠ABD+∠DBC=180°可得∠DBN+∠DBM=∠MBN=90°,即可得答案.
(1)解:在△ABE和△DBC中 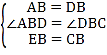 ,
,
∴△ABE≌△DBC
(2)解:△MBN是等腰直角三角形,證明如下:
∵△ABE≌△DBC,
∴AE=CD,∠BAM=∠BDN.
∵M,N分別是AE,CD的中點,
∴AM=![]() AE,CN=
AE,CN=![]() CD.
CD.
∴AM=CN.
在△ABM和△DBN中  ,
,
∴ABM≌△DBN.
∴BM=BN,∠ABM=∠DBN.
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠ABM+∠DBM=90°.
∴∠DBN+∠DBM=∠MBN=90°.
∴△MBN是等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,PA切⊙O于點A,PO交⊙O于點C,連接BC,∠P=∠B. 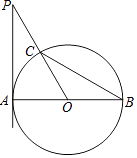
(1)求∠P的度數;
(2)連接PB,若⊙O的半徑為a,寫出求△PBC面積的思路. 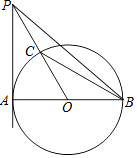
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在面積為6的Rt△ABC中,∠C=90°,AC=4,AB=5,BC邊上有一動點P,當點P到AB邊的距離等于PC的長時,那么點P到端點B的距離等于( )
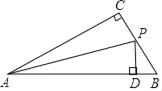
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了發展鄉村旅游,洪江村準備在洪江河道上修一座與河道垂直的吊橋,如圖1所示,直線l、m代表洪江河的兩岸,且l∥m,點A是洪江村自助農場的所在地,點B是洪江村游樂園所在地.
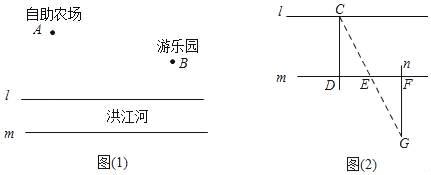
問題1:吊橋的選址
吊橋準備選在到A、B兩地的距離之和剛好為最小的點C處,即在直線l上找到使(AC+BC)的值為最小的點C的位置.請利用你所學的知識幫助村委會設計選址方案(直接在圖1里作圖),并簡單說明你所設計方案的原理
問題2:河道的寬度
在測量河道的寬度時,施工隊在河道南側的開闊地用以下方法(如圖2所示):①作CD⊥1,與河對岸的直線m相交于D;②在直線m上取E、F兩點,使得DE=EF=10米;③過點F作m的垂線n;④在直線n上找到一點G,使得點G與C、E兩點在同一直線上;⑤測量FG的長度為20米.請問你知道河道的寬度嗎?說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板按如圖擺放,其中△ABC為含有45度角的三角板,直線AD是等腰直角三角形ABC的對稱軸,且將△ABC分成兩個等腰直角三角形,DM、DN分別與邊AB、AC交于E、F兩點,有下列四個結論:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四邊形AEDF=![]() AB2.其中正確結論是_____(填寫正確序號)
AB2.其中正確結論是_____(填寫正確序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】試驗與探究:我們知道分數![]() 寫為小數即
寫為小數即![]() ,反之,無限循環小數
,反之,無限循環小數![]() 寫成分數即
寫成分數即![]() .一般地,任何一個無限循環小數都可以寫成分數形式.現在就以
.一般地,任何一個無限循環小數都可以寫成分數形式.現在就以![]() 為例進行討論:設
為例進行討論:設![]() =x,由
=x,由![]() =0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得
=0.7777…,可知,10x﹣x=7.77…﹣0.777…=7,即10x﹣x=7,解方程得![]() ,于是得
,于是得![]() =
=![]() .
.
請仿照上述例題完成下列各題:
(1)請你把無限循環小數![]() 寫成分數,即
寫成分數,即![]() =_____.
=_____.
(2)你能化無限循環小數![]() 為分數嗎?請仿照上述例子求解之.
為分數嗎?請仿照上述例子求解之.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y= ![]() (x>0)的圖象與矩形OABC對角線的交點為M,分別與AB,BC交于點D,E,連接OD,OE,則
(x>0)的圖象與矩形OABC對角線的交點為M,分別與AB,BC交于點D,E,連接OD,OE,則 ![]() = , 當k=4時,四邊形ODBE的面積為平方單位.
= , 當k=4時,四邊形ODBE的面積為平方單位. 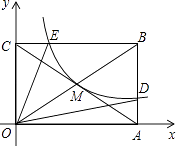
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AC為直徑作⊙O交BC于點D,過點D作EF⊥AB于點F,交AC的延長線于點E. 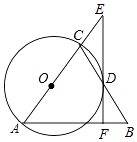
(1)判斷EF與⊙O的位置關系,并說明理由;
(2)若AF=6,sinE= ![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是等邊三角形ABC內一點,將線段AD繞點A順時針旋轉60°,得到線段AE,連接CD,BE.
(1)求證:∠AEB=∠ADC;
(2)連接DE,若∠ADC=105°,求∠BED的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com