
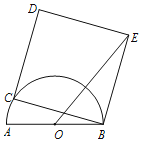
【題目】如圖,點C是半圓![]() 上一動點,以BC為邊作正方形BCDE,使
上一動點,以BC為邊作正方形BCDE,使![]() 在正方形內,連OE,若AB=4cm,則OD的最大值為_____________cm.
在正方形內,連OE,若AB=4cm,則OD的最大值為_____________cm.
科目:初中數學 來源: 題型:
【題目】隨著移動互聯網的快速發展,基于互聯網的共享單車應運而生.為了解某小區居民使用共享單車的情況,某研究小組隨機采訪該小區的10位居民,得到這10位居民一周內使用共享單車的次數分別為:17,12,15,20,17,0,7,26,17,9.
(1)這組數據的中位數是 ,眾數是 ;
(2)計算這10位居民一周內使用共享單車的平均次數;
(3)若該小區有200名居民,試估計該小區居民一周內使用共享單車的總次數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀題.
材料一:若一個整數m能表示成a2-b2(a,b為整數)的形式,則稱這個數為“完美數”.例如,3=22-12,9=32-02,12=42-22,則3,9,12都是“完美數”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整數),所以M也是”完美數”.
材料二:任何一個正整數n都可以進行這樣的分解:n=p×q(p、q是正整數,且p≤q).如果p×q在n的所有這種分解中兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解,并且規定F(n)=![]() .例如18=1×18=2×9=3×6,這三種分解中3和6的差的絕對值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,這三種分解中3和6的差的絕對值最小,所以就有F(18)=![]() .請解答下列問題:
.請解答下列問題:
(1)8______(填寫“是”或“不是”)一個完美數,F(8)= ______.
(2)如果m和n都是”完美數”,試說明mn也是完美數”.
(3)若一個兩位數n的十位數和個位數分別為x,y(1≤x≤9),n為“完美數”且x+y能夠被8整除,求F(n)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
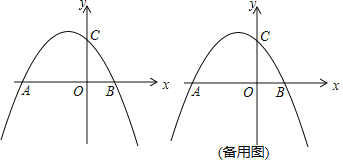
【題目】如圖,二次函數![]() 的圖象與
的圖象與![]() 軸交于點A、B,與y軸交于點C,點A的坐標為(-4,0),P是拋物線上一點 (點P與點A、B、C不重合).
軸交于點A、B,與y軸交于點C,點A的坐標為(-4,0),P是拋物線上一點 (點P與點A、B、C不重合).
(1)b= ,點B的坐標是 ;
(2)設直線PB直線AC交于點M,是否存在這樣的點P,使得PM:MB=1:2?若存在,求出點P的橫坐標;若不存在,請說明理由;
(3)連接AC、BC,判斷∠CAB和∠CBA的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點C順時針旋轉90°得到△EDC.若點A,D,E在同一條直線上,∠ACB=20°,則∠ADC的度數是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象對稱軸為x=![]() ,圖象交x軸于A,B,交y軸于C(0,-3),且AB=5,直線y=kx+b(k>0)與二次函數圖象交于M,N(M在N的右邊),交y軸于P.
,圖象交x軸于A,B,交y軸于C(0,-3),且AB=5,直線y=kx+b(k>0)與二次函數圖象交于M,N(M在N的右邊),交y軸于P.
(1)求二次函數圖象的解析式;
(2)若b=-5,且△CMN的面積為3,求k的值;
(3)若b=-3k,直線AN交y軸于Q,求![]() 的值或取值范圍.
的值或取值范圍.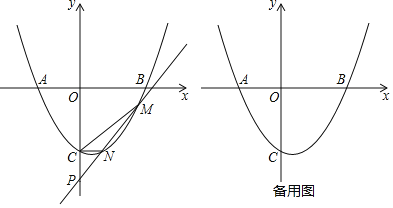
查看答案和解析>>
科目:初中數學 來源: 題型:
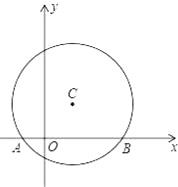
【題目】.如圖,在平面直角坐標系中,以點C(1,1)為圓心,2為半徑作圓,交x軸于A,B兩點,點P在優弧![]() 上.
上.
(1)求出A,B兩點的坐標;
(2)試確定經過A、B且以點P為頂點的拋物線解析式;
(3)在該拋物線上是否存在一點D,使線段OP與CD互相平分?若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是邊AB上一點,以BD為直徑的⊙O經過點E,且交BC于點F.
(1)求證:AC是⊙O的切線;
(2)若BF=6,⊙O的半徑為5,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某銷售商準備在南充采購一批絲綢,經調查,用10000元采購A型絲綢的件數與用8000元采購B型絲綢的件數相等,一件A型絲綢進價比一件B型絲綢進價多100元.
(1)求一件A型、B型絲綢的進價分別為多少元?
(2)若銷售商購進A型、B型絲綢共50件,其中A型的件數不大于B型的件數,且不少于16件,設購進A型絲綢m件.
①求m的取值范圍.
②已知A型的售價是800元/件,銷售成本為2n元/件;B型的售價為600元/件,銷售成本為n元/件.如果50≤n≤150,求銷售這批絲綢的最大利潤w(元)與n(元)的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com