
【題目】(1)在![]() 中,
中,![]() ,
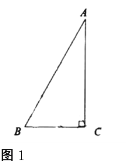
,![]() (如圖1),
(如圖1),![]() 與
與![]() 有怎樣的數量關系?試證明你的結論.
有怎樣的數量關系?試證明你的結論.
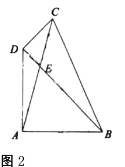
(2)圖2,在四邊形![]() 中,
中,![]() 相于點
相于點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 長.
長.
【答案】(1)AB=2BC,證明見解析;(2)![]() -1.
-1.
【解析】
(1)取AB的中點D,連接DC,得AD=BD=CD,再證明△DBC是等邊三角形得BD=BC,從而可證明AB=2BC;
(2)過點A作AF⊥BD于點F,先確定∠2及∠3的度數,在Rt△AFB中求出AF,BF;Rt△AEF中,求出EF,AE,在Rt△ABD中求出DB,繼而得出DE.
(1)AB=2BC
證明:取AB的中點D,連接DC,
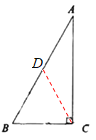
∵∠ACB=90°,CD為斜邊AB上的中線
∴AD=BD=CD
∴∠A=∠ACD=30°,∠B=∠BCD
∴∠ADC=180°-∠A-∠ACD=120°
∴∠B=∠BCD=![]() ∠ADC=60°
∠ADC=60°
∴△DBC是等邊三角形
∴BD=BC
∴AB=2BD=2BC
即AB=2BC
(2)過點A作AF⊥BD于點F,
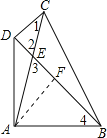
∵∠CDB=90°,∠1=30°,
∴∠2=∠3=60°,
在△AFB中,∠AFB=90°,
∵∠4=45°,AB=![]() ,
,
∴AF=BF=![]() ,
,
在Rt△AEF中,∠AFE=90°,
∴EF=1,AE=2,
在△ABD中,∠DAB=90°,AB=![]() ,
,
∴DB=2![]() ,
,
∴DE=DB-BF-EF=![]() -1.
-1.


科目:初中數學 來源: 題型:
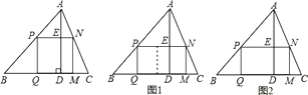
【題目】課本中有一道作業題:有一塊三角形余料ABC,它的邊BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一邊在BC上,其余兩個頂點分別在AB,AC上.
(1)加工成的正方形零件的邊長是多少mm?
(2)如果原題中要加工的零件是一個矩形,且此矩形是由兩個并排放置的正方形所組成,如圖1,此時,這個矩形零件的兩條邊長又分別為多少?請你計算.
(3)如果原題中所要加工的零件只是一個矩形,如圖2,這樣,此矩形零件的兩條邊長就不能確定,但這個矩形面積有最大值,求達到這個最大值時矩形零件的兩條邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小華和小亮想用所學的數學知識測量家門前小河的寬.測量時,他們選擇了河對岸邊的一棵大樹,將其底部作為點A,在他們所在的岸邊選擇了點B,使得AB與河岸垂直,并在B點豎起標桿BC,再在AB的延長線上選擇點D豎起標桿DE,使得點E與點C、A共線.
已知:CB⊥AD,ED⊥AD,測得BC=1m,DE=1.5m,BD=8.5m.測量示意圖如圖所示.請根據相關測量信息,求河寬AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
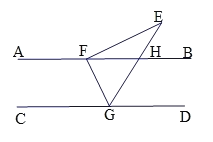
【題目】如圖,AB// CD,Rt△EFG的頂點F,G分別落在直線AB,CD上,GE交AB于點H,∠EFG=90°,∠E=32°.
(1)∠FGE= °
(2)若GE平分∠FGD,求∠EFB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)畫出△ABC向下平移4個單位長度得到的△A1B1C1,點C1的坐標是 ;
(2)以點B為位似中心,在網格內畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2:1;
(3)四邊形AA2C2C的面積是 平方單位.

查看答案和解析>>
科目:初中數學 來源: 題型:
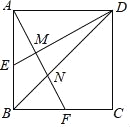
【題目】正方形ABCD的邊長AB=2,E為AB的中點,F為BC的中點,AF分別與DE、BD相交于點M,N,則MN的長為( )
A. ![]() B.
B. ![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有3張邊長為![]() 的正方形紙片(
的正方形紙片(![]() 類),5張邊長為
類),5張邊長為![]() 的矩形紙片(
的矩形紙片(![]() 類),5張邊長為
類),5張邊長為![]() 的正方形紙片(
的正方形紙片(![]() 類).
類).
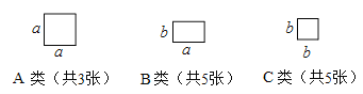
我們知道:多項式乘法的結果可以利用圖形的面積表示.
例如:![]() 就能用圖①或圖②的面積表示.
就能用圖①或圖②的面積表示.
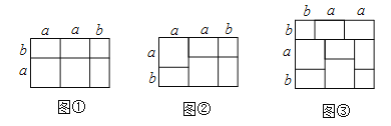
(1)請你寫出圖③所表示的一個等式:_______________;
(2)如果要拼一個長為![]() ,寬為
,寬為![]() 的長方形,則需要
的長方形,則需要![]() 類紙片_____張,需要
類紙片_____張,需要![]() 類紙片_____張,需要
類紙片_____張,需要![]() 類紙片_____張;
類紙片_____張;
(3)從這13張紙片中取出若干張,每類紙片至少取出一張,把取出的這些紙片拼成一個正方形(按原紙張進行無縫隙,無重疊拼接),則拼成的正方形的邊長最長可以是_______(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:如果兩個等腰三角形的頂角相等,且項角的頂點互相重合,則稱此圖形為“手拉手全等模型”.因為頂點相連的四條邊,形象的可以看作兩雙手,所以通常稱為“手拉手模型”.例如,如(1),![]() 與
與![]() 都是等腰三角形,其中
都是等腰三角形,其中![]() ,則△ABD≌△ACE(SAS).
,則△ABD≌△ACE(SAS).
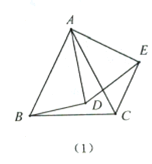
(1)熟悉模型:如(2),已知![]() 與
與![]() 都是等腰三角形,AB=AC,AD=AE,且
都是等腰三角形,AB=AC,AD=AE,且![]() ,求證:
,求證:![]() ;
;
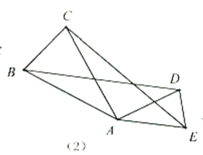
(2)運用模型:如(3),![]() 為等邊
為等邊![]() 內一點,且
內一點,且![]() ,求
,求![]() 的度數.小明在解決此問題時,根據前面的“手拉手全等模型”,以
的度數.小明在解決此問題時,根據前面的“手拉手全等模型”,以![]() 為邊構造等邊
為邊構造等邊![]() ,這樣就有兩個等邊三角形共頂點
,這樣就有兩個等邊三角形共頂點![]() ,然后連結
,然后連結![]() ,通過轉化的思想求出了
,通過轉化的思想求出了![]() 的度數,則
的度數,則![]() 的度數為 度;
的度數為 度;
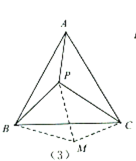
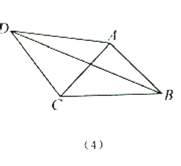
(3)深化模型:如(4),在四邊形![]() 中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求
中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和他的同學根據拋擲兩枚硬幣時記錄的實驗結果,制作“出現兩個正面”的頻數、頻率表如下:
拋擲次數 |
|
|
|
|
|
|
|
| |
出現兩個正面的頻數 |
|
|
|
|
|
|
|
| |
出現兩個正面的頻率 |
|
|
|
|
|
|
|
|
![]() 在大數次拋擲兩枚硬幣的實驗中,出現兩個正面的頻率穩定在________附近;
在大數次拋擲兩枚硬幣的實驗中,出現兩個正面的頻率穩定在________附近;
![]() 小明和表弟玩一個拋擲兩枚硬幣的游戲,小明制定的游戲規則如下:拋出兩個正面–小明的表弟贏
小明和表弟玩一個拋擲兩枚硬幣的游戲,小明制定的游戲規則如下:拋出兩個正面–小明的表弟贏![]() 分;拋出其他結果–小明贏
分;拋出其他結果–小明贏![]() 分;誰先到
分;誰先到![]() 分,誰就得勝.你認為這個游戲規則公平嗎?說說理由.
分,誰就得勝.你認為這個游戲規則公平嗎?說說理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com