
【題目】在平面直角坐標系xOy中,直線y4x4與x軸,y軸分別交于點A,B,點A在拋物線yax2bx3a(a0)上,將點B向右平移3個單位長度,得到點C.
(1)拋物線的頂點坐標為 (用含a的代數式表示)
(2)若a1,當t-1≤x≤t時,函數yax2bx3a(a0)的最大值為y1,最小值為y2,且y1y22,求t的值;
(3)若拋物線與線段BC恰有一個公共點,結合函數圖象,求a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 時,拋物線與線段
時,拋物線與線段![]() 有一個交點.
有一個交點.
【解析】
(1)將A(-1,0)代入拋物線得b=-2a,再將拋物線解析式化為頂點式即可求解;
(2)當a=-1時,拋物線頂點坐標為(1,4),然后分情況根據拋物線的性質即可解答;
(3)先求點B坐標,將點B向右平移3個單位長度,得到點C,利用拋物線的頂點坐標求解.
解:(1)直線y=4x+4與x軸,y軸分別交于點A,B,
∴A(-1,0),B(0,4),
點A在拋物線y=ax2+bx-3a(a<0)上,
∴b=-2a,
∴拋物線y=ax2+bx-3a=a(x-1)2-4a,
∴拋物線的頂點坐標為(1,-4a).
故答案為:![]() ;
;
(2)∵![]() ,
,
∴拋物線的解析式為![]() .
.
①當![]() 時,
時,
![]() ,
,
∴![]() .
.
②當![]() 時,即
時,即![]() 時,
時,![]() .
.
∴![]() .
.
③當![]() 時,
時,![]() .
.
解得,![]() (舍去).
(舍去).
④當![]() 時,
時,![]() .
.
解得,![]() (舍去).
(舍去).
∴![]() 或
或![]() .
.
(3)①把![]() 代入拋物線,得
代入拋物線,得![]() .
.
∵拋物線與線段![]() 只有一個公共點,
只有一個公共點,
∴![]() .
.
∴![]() .
.
②當拋物線頂點在線段![]() 上時,則頂點坐標為
上時,則頂點坐標為![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 或
或![]() 時,拋物線與線段
時,拋物線與線段![]() 有一個交點.
有一個交點.


科目:初中數學 來源: 題型:
【題目】 鄭州外國語中學為了解學生課下閱讀所用時間的情況,從各年級學生中隨機抽查了一部分學生進行統計,下面是針對此次統計所制作的不完整的頻數分布表和頻數分布直方圖,請根據圖表信息回答下列問題:
組別 | 時間段(小時) | 頻數 | 頻率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
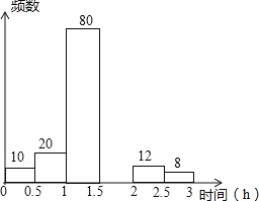
(1)表中a=______b=______;
(2)請補全頻數分布直方圖;
(3)樣本中,學生日閱讀所用時間的中位數落在第______組;
(4)該校共有學生3000人,請估計學生日閱讀量不少于1.5小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,過點
上的點,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,以
,以![]() 為直徑作半圓
為直徑作半圓![]() .
.
(1)填空:點![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;當
上;當![]() 時,
時,![]() 的值是_____________;
的值是_____________;
(2)如圖1,在![]() 中,當
中,當![]() 時,求證:
時,求證:![]() ;
;
(3)如圖2,當![]() 的頂點
的頂點![]() 是邊
是邊![]() 的中點時,請直接寫出
的中點時,請直接寫出![]() 三條線段的數量關系.
三條線段的數量關系.
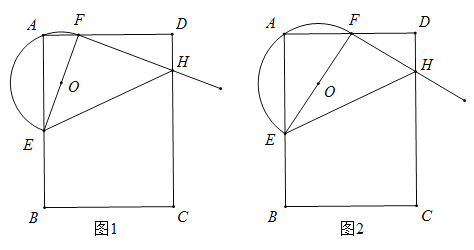
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】茶葉是安徽省主要經濟作物之一,2020年新茶上市期間,某茶廠為獲得最大利益,根據市場行情,把新茶價格定為400元/kg,并根據歷年的相關數據整理出第x天(1≤x≤15,且x為整數)制茶成本(含采摘和加工)和制茶量的相關信息如下表.假定該茶廠每天制作和銷售的新茶沒有損失,且能在當天全部售出(當天收入=日銷售額-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出該茶廠第10天的收入;
(2)設該茶廠第x天的收入為y(元).試求出y與x之間的函數關系式,并求出y的最大值及此時x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為3cm,E為CD邊上一點,∠DAE=30°,M為AE的中點,過點M作直線分別與AD、BC相交于點P、Q.若PQ=AE,則AP等于 cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BA=BC,以AB為直徑的⊙O分別交AC,BC于點D,E,BC的延長線與⊙O的切線AF交于點F.
(1)求證:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的長.
,CE:EB=1:4,求CE,AF的長.
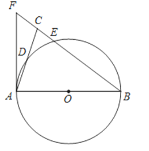
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊上的一個動點,將四邊形
邊上的一個動點,將四邊形![]() 沿直線
沿直線![]() 折疊,得到四邊形
折疊,得到四邊形![]() ,點
,點![]() 、
、![]() 的對應點分別為點
的對應點分別為點![]() 、
、![]() .直線
.直線![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)連接![]() ,已知
,已知![]() .
.
①如圖①,當![]() ,
,![]() 時,求
時,求![]() 的長度;
的長度;
②如圖②,當四邊形![]() 為菱形時,請直接寫出
為菱形時,請直接寫出![]() 的長度.
的長度.
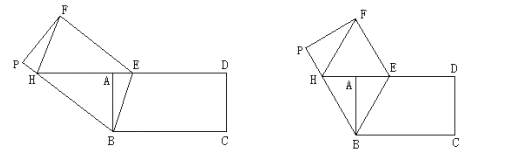
圖① 圖②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 有一種用“☆”定義的新運算,對于任意實數a,b,都有a☆b=b2+2a+1.例如7☆4=42+2×7+1=31.
(1)已知﹣m☆3的結果是﹣4,則m= .
(2)將兩個實數2n和n﹣2用這種新定義“☆”加以運算,結果為9,則n的值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個函數,自變量x取a時,函數值y也等于a,我們稱a為這個函數的不動點.如果二次函數y=x2+2x+c有兩個相異的不動點x1、x2,且x1<1<x2,則c的取值范圍是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com