
如圖,科技小組準(zhǔn)備用材料圍建一個面積為60m2的矩形科技園ABCD,其中一邊AB靠墻,墻長為12m。設(shè)AD的長為xm,DC的長為ym。
(1)求y與x之間的函數(shù)關(guān)系式;
(2)若圍成矩形科技園ABCD的三邊材料總長不超過26m,材料AD和DC的長都是整米數(shù),求出滿足條件的所有圍建方案。
 開心練習(xí)課課練與單元檢測系列答案
開心練習(xí)課課練與單元檢測系列答案 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,點A在反比例函數(shù) 的圖象上.
的圖象上.
(1) 求反比例函數(shù) 的解析式;
的解析式;
(2)在y軸上是否存在點P,使得△AOP是直角三角形?若存在,直接寫出P點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系中,一次函數(shù) 的圖象與反比例函數(shù)
的圖象與反比例函數(shù) 的圖象在第一象限內(nèi)交于點
的圖象在第一象限內(nèi)交于點 ,與
,與 軸交于點
軸交于點 ,與
,與 軸交于點
軸交于點 ,
, 。
。
(1)求一次函數(shù)和反比例函數(shù)的解析式;
(2)若在 軸上存在點
軸上存在點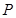 ,使得
,使得 ,求點
,求點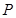 的坐標(biāo)。
的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,函數(shù)y1=-x+4的圖象與函數(shù)y2= (x>0)的圖象交于 A(a,1)、B(1,b)兩點.
(x>0)的圖象交于 A(a,1)、B(1,b)兩點.
(1)求a,b及y2的函數(shù)關(guān)系式;
(2)觀察圖象,當(dāng)x>0時,比較y1與y2大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系中,反比例函數(shù) (x>0)的圖象和矩形ABCD的第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標(biāo)為(2,6) .
(x>0)的圖象和矩形ABCD的第一象限,AD平行于x軸,且AB=2,AD=4,點A的坐標(biāo)為(2,6) .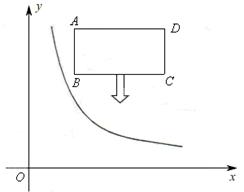
(1)直接寫出B、C、D三點的坐標(biāo);
(2)若將矩形向下平移,矩形的兩個頂點恰好同時落在反比例函數(shù)的圖象上,猜想這是哪兩個點,并求矩形的平移距離和反比例函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,平面直角坐標(biāo)系中,直線 與x軸交于點A,與雙曲線
與x軸交于點A,與雙曲線 在第一象限內(nèi)交于點B,BC丄x軸于點C,OC=2AO.求雙曲線的解析式.
在第一象限內(nèi)交于點B,BC丄x軸于點C,OC=2AO.求雙曲線的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系 中,直線AB與
中,直線AB與 軸交于點A,與
軸交于點A,與 軸交于點C(
軸交于點C( ,
, ),且與反比例 函數(shù)
),且與反比例 函數(shù)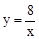 在第一象限內(nèi)的圖象交于點B,且BD⊥
在第一象限內(nèi)的圖象交于點B,且BD⊥ 軸于點D,OD
軸于點D,OD .
.
(1)求直線AB的函數(shù)解析式;
(2)設(shè)點P是 軸上的點,若△PBC的面積等于
軸上的點,若△PBC的面積等于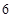 ,直接寫出點P的坐標(biāo).
,直接寫出點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,將邊長為4的等邊三角形AOB放置于平面直角坐標(biāo)系xoy中,F(xiàn)是AB邊上的動點(不與端點A、B重合),過點F的反比例函數(shù) (k>0,x>0)與OA邊交于點E,過點F作FC⊥x軸于點C,連結(jié)EF、OF.
(k>0,x>0)與OA邊交于點E,過點F作FC⊥x軸于點C,連結(jié)EF、OF.
(1)若S△OCF= ,求反比例函數(shù)的解析式;
,求反比例函數(shù)的解析式;
(2)在(1)的條件下,試判斷以點E為圓心,EA長為半徑的圓與y軸的位置關(guān)系,并說明理由;
(3)AB邊上是否存在點F,使得EF⊥AE?若存在,請求出BF:FA的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
如圖所示的圓柱體中底面圓的半徑是 ,高為2,若一只小蟲從A點出發(fā)沿著圓柱體的側(cè)面爬行到C點,則小蟲爬行的最短路程是 _________ .(結(jié)果保留根號)
,高為2,若一只小蟲從A點出發(fā)沿著圓柱體的側(cè)面爬行到C點,則小蟲爬行的最短路程是 _________ .(結(jié)果保留根號)

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com