Question

【題目】在△ABC中，以線段AB為邊作△ABD，使得AD=BD，連接DC，再以DC為邊作△CDE，使得DC=DE，∠CDE=∠ADB=a。

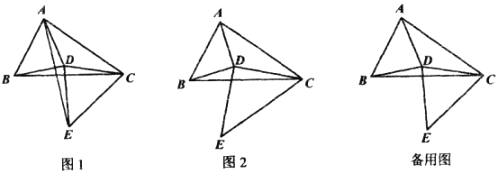
（1）如圖1，連結AE，求證：AE=BC；

（2）如圖2，BC=4時，將線段CB沿著射線CE的方向平移，得到線段EF，連接BF，AF。

①若=90°，依題意補全圖2，求線段AF的長；

②請直接寫出線段AF的長（用含的式子表示）。

Answer 1

【答案】（1）證明見解析；

（2）補全圖形見解析，AF的長為

（3）AF的長為8sin

【解析】分析(1)由∠ADB=∠CDE，可得∠ADE=∠BDC，據SAS得到△ADE≌△BDC，從而得證.（2）①設DE與BC相交于點H，連接 AE，交BC于點G，根據SAS推出△ADE≌△BDC，根據全等三角形的性質得出AE=BC，∠AED=∠BCD．求出∠AFE=45°，解直角三角形求出即可；②過E作EM⊥AF于M，根據等腰三角形的性質得出∠AEM=∠FEM= ，AM=FM，解直角三角形求出FM即可．

本題解析: 分析：（1）（1）∵∠ADB=∠CDE，

∴∠ADB+∠BDE=∠CDE+∠BDE,∴∠ADE=∠BDC,

在△ADE與△BDC中，

∵

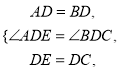
∴△ADE≌△BDC。∴AE=BC

（2）①補全圖形。設DE與BC相交于點H，連接AE，交BC于點G，如圖:

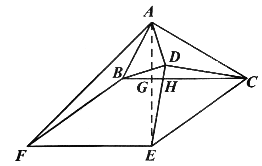
由（1）得△ADE≌△BDC。∴∠AED=∠BCD。

∵DE與BC相交于點H，∴∠GHE=∠DHC。

∴∠EGH=∠EDC=90°。

∵線段CB沿著射線CE的方向平移，得到線段EF，

∴EF=CB=4，EF∥CB。∴AE=EF。

∵CB∥EF，∴∠AEF=∠EGH=90°。

∵AE=EF，∠AEF=90°，∴∠AFE=45°。

∴AF=。

②如圖2，

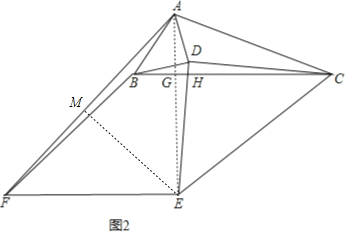
過E作EM⊥AF于M，∵由①知：AE=EF=BC，

∴∠AEM=∠FEM=，AM=FM，∴AF=2FM=EF×sin=8sin.