
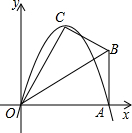
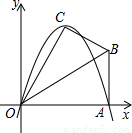
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內.將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.

(1)求點C的坐標;
(2)若拋物線y=ax2+bx(a≠0)經過C、A兩點,求此拋物線的解析式;
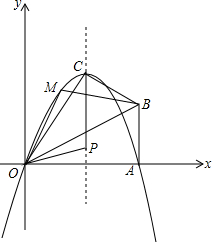
(3)若拋物線的對稱軸與OB交于點D,點P為線段DB上一點,過P作y軸的平行線,交拋物線于點M.問:是否存在這樣的點P,使得四邊形CDPM為等腰梯形?若存在,請求出此時點P的坐標;若不存在,請說明理由.
注:拋物線y=ax2+bx+c(a≠0)的頂點坐標為![]() ,對稱軸公式為
,對稱軸公式為![]()
|
解:(1)過點C作CH⊥x軸,垂足為H ∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2 ∴OB=4,OA= 由折疊知,∠COB=300,OC=OA= ∴∠COH=60°,OH= ∴C點坐標為( (2)∵拋物線 ∴ ∴此拋物線的解析式為: (3)存在.因為 MP⊥ ∴P( 作PQ⊥CD,垂足為Q,ME⊥CD,垂足為E 把 ∴M( 同理:Q( 要使四邊形CDPM為等腰梯形,只需CE=QD 即 ∴P點坐標為( ∴存在滿足條件的點P,使得四邊形CDPM為等腰梯形,此時P點的坐為( |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
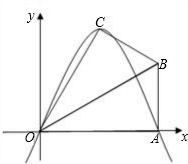 線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內.將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內.將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.查看答案和解析>>
科目:初中數學 來源: 題型:
 .問:是否存在這樣的點P,使得四邊形CDPM為等腰梯形?若存在,請求出此時點P的坐標;若不存在,請說明理由.
.問:是否存在這樣的點P,使得四邊形CDPM為等腰梯形?若存在,請求出此時點P的坐標;若不存在,請說明理由.| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•武漢模擬)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 為原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
(2013•武漢模擬)已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 為原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•六盤水)已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2
(2013•六盤水)已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2| 3 |
查看答案和解析>>
科目:初中數學 來源:第34章《二次函數》常考題集(23):34.4 二次函數的應用(解析版) 題型:解答題
 ,對稱軸公式為x=-
,對稱軸公式為x=-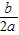 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com