
【題目】如圖,已知△ABC的周長是21,BO、CO分別平分∠ABC和∠ACB,OD⊥BC于D,OE⊥AB,OF⊥AC,且OD=3.
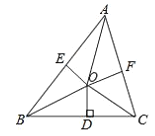
(1)試判斷線段OD、OE、OF的大小關系.
(2)求△ABC的面積.
【答案】(1)OD=OE=OF,理由見解析;(2)31.5.
【解析】
(1)根據角平分線上的點到角兩邊的距離相等即可得出OD、OE、OF的大小關系;
(2)由S△ABC=S△BOC+ S△AOB+ S△AOC,利用三角形的面積公式進行求解即可.
解:(1)OD=OE=OF,理由如下:
∵BO平分∠ABC,OD⊥BC,OE⊥AB,
∴OD=OE,
∵CO平分∠ACB,OD⊥BC,OF⊥AC,
∴OD=OF,
∴OD=OE=OF;
(2)∵S△ABC=S△BOC+ S△AOB+ S△AOC,
S△BOC=![]() ,S△AOB=
,S△AOB=![]() , S△AOC=
, S△AOC=![]() ,
,
∴S△ABC=![]() +
+![]() +
+![]() ,
,
∵OD=OE=OF,
∴S△ABC=![]() (BC+AB+AC),
(BC+AB+AC),
∵AB+BC+AC=21,OD=3,
∴S△ABC=![]() =31.5.
=31.5.


科目:初中數學 來源: 題型:
【題目】已知用2輛A型車和1輛B型車載滿貨物一次可運貨物10噸;用1輛A型車和2輛B型車載滿貨物一次可運貨11噸.某物流公司現有31噸貨物,計劃同時租用A型車a輛,B型車b輛,一次運完,且恰好每輛車都載滿貨物.根據以上信息,解答下列問題:
(1)用1輛A型車和1輛B型車都載滿貨物一次可分別運貨多少噸?
(2)請你幫該物流公司設計租車方案.若A型車每輛需租金100元/次,B型車每輛需租金120元/次.請選出最省錢的租車方案,并求出最少租車費.
查看答案和解析>>
科目:初中數學 來源: 題型:
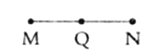
【題目】如圖,已知線段![]() ,點
,點![]() 是線段
是線段![]() 的中點,先按要求畫圖形,再解決問題.
的中點,先按要求畫圖形,再解決問題.
(1)延長線段![]() 至點
至點![]() ,使
,使![]() ;延長線段
;延長線段![]() 至點
至點![]() ,使
,使![]() ;(尺規作圖,保留作圖痕跡)
;(尺規作圖,保留作圖痕跡)
(2)求線段![]() 的長度;
的長度;
(3)若點![]() 是線段
是線段![]() 的中點,求線段
的中點,求線段![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】足球訓練中,為了訓練球員快速搶斷轉身,教練在東西方向的足球場上畫了一條直線,要求球員在這條直線上進行折返跑訓練,如果約定向西為正,向東為負,將某球員的一組折返距練習記錄如下(單位:米) :![]() ,
,![]() .
.
![]() 球員最后到達的地方在出發點的哪個方向?距出發點多遠?
球員最后到達的地方在出發點的哪個方向?距出發點多遠?
![]() 球員訓練過程中,最遠處離出發點 米?
球員訓練過程中,最遠處離出發點 米?
![]() 球員在這一組練習過程中,共跑了多少米?
球員在這一組練習過程中,共跑了多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC 的角平分線與 BC 的垂直平分線交于點 D,DE⊥AB, DF⊥AC,垂足分別為 E,F.若 AB=10,AC=8,求 BE 長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:如果![]() ,那么稱b為n的布谷數,記為
,那么稱b為n的布谷數,記為![]() .
.
例如:因為![]() ,所以
,所以![]() ,
,
因為![]() ,
,
所以![]() .
.
(1)根據布谷數的定義填空:g(2)=________________,g(32)=___________________.
(2)布谷數有如下運算性質:
若m,n為正整數,則![]() ,
,![]() .
.
根據運算性質解答下列各題:
①已知![]() ,求
,求![]() 和
和![]() 的值;
的值;
②已知![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是最大的負整數,
是最大的負整數,![]() ,C是-4的相反數,且
,C是-4的相反數,且![]() 、
、![]() 、
、![]() 分別是點
分別是點![]() 、
、![]() 、
、![]() 在數軸上對應的數.
在數軸上對應的數.
![]()
(1)求![]() 、
、![]() 、
、![]() 的值,并在數軸上標出點
的值,并在數軸上標出點![]() 、
、![]() 、
、![]() .
.
(2)在數軸上,若![]() 到
到![]() 的距離剛好是3,則
的距離剛好是3,則![]() 點叫做
點叫做![]() 的“幸福點”則
的“幸福點”則![]() 的幸福點
的幸福點![]() 所表示的數應該是_________.
所表示的數應該是_________.
(3)若動點![]() 從點
從點![]() 出發沿數軸向正方向運動,動點
出發沿數軸向正方向運動,動點![]() 同時從點
同時從點![]() 出發也沿數軸向正方向運動,點
出發也沿數軸向正方向運動,點![]() 的速度是每秒3個單位長度,點
的速度是每秒3個單位長度,點![]() 的速度是每秒1個單位長度,求運動幾秒后,點
的速度是每秒1個單位長度,求運動幾秒后,點![]() 可以追上點
可以追上點![]() .
.
(4)在數軸上,若![]() 到
到![]() 、
、![]() 的距離之和為6,則
的距離之和為6,則![]() 叫做
叫做![]() 、
、![]() 的幸福中心”請直接寫出所有點
的幸福中心”請直接寫出所有點![]() 在數軸上對應的數.
在數軸上對應的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖 ,AD 是∠BAC 的平分線,且 DF⊥AC 于 F,∠B=90°,DE=DC.

(1)求證:BE=CF.
(2)若△ADE 和△DCF 的面積分別是12和5,求△ABC 的面積.
(3)請你寫出∠BAC與∠CDE有什么數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對任意一個兩位數![]() ,如果
,如果![]() 滿足個位數字與十位數字互不相同,且都不為零,那么稱這個兩位數為“迥異數”,將一個“迥異數”的個位數字與十位數字對調后得到一個新的兩位數,把這個新兩位數與原兩位數的和與11的商記為
滿足個位數字與十位數字互不相同,且都不為零,那么稱這個兩位數為“迥異數”,將一個“迥異數”的個位數字與十位數字對調后得到一個新的兩位數,把這個新兩位數與原兩位數的和與11的商記為![]() .例如:
.例如:![]() ,對調個位數字與十位數字得到新兩位數21,新兩位數與原兩位數的和為21+12=33,和與11的商為33÷11=3,所以
,對調個位數字與十位數字得到新兩位數21,新兩位數與原兩位數的和為21+12=33,和與11的商為33÷11=3,所以![]() .根據以上定義,回答下列問題:
.根據以上定義,回答下列問題:
(1)填空:①下列兩位數:40,42,44中,“迥異數”為_______;②計算:![]() =_______;
=_______;
(2)如果一個“迥異數”![]() 的十位數字是
的十位數字是![]() ,個位數字是
,個位數字是![]() ,且
,且![]() ,請求出“迥異數”
,請求出“迥異數”![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com