
【題目】已知:![]() 為
為![]() 的直徑,
的直徑,![]() 為圓弧上一點,
為圓弧上一點,![]() 垂直于過
垂直于過![]() 點的切線,垂足為
點的切線,垂足為![]() ,
,![]() 的延長線交直線
的延長線交直線![]() 于點
于點![]() .
.![]() ,垂足為點
,垂足為點![]() .
.
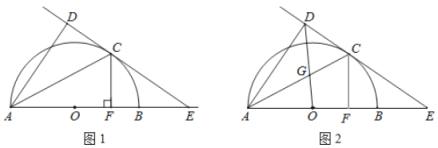
(1)如圖1,求證:![]() ;
;
(2)如圖2,若![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,且
,且![]() 時,求
時,求![]() 的長度.
的長度.
【答案】(1)見解析;(2)![]() .
.
【解析】
1)連結(jié)OC,如圖1,先利用切線的性質(zhì)得到OC⊥CD,再判斷OC∥AD得到∠1=∠3,加上∠2=∠3,則有∠1=∠2,于是可判斷![]() ,即可得到
,即可得到![]() ;
;
(2)連結(jié)OC,如圖2,先證明△OCG∽△DAG得到![]() ,即可求出
,即可求出![]() =10,Rt△OCF中利用勾股定理即可求出
=10,Rt△OCF中利用勾股定理即可求出![]() .
.
(1)連結(jié)![]() ,
,
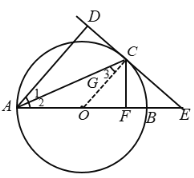
∵直線![]() 與
與![]() 相切于點
相切于點![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∴在![]() 和
和![]() 中
中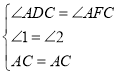
∴![]()
∴![]()
(2)連結(jié)![]() ,
,
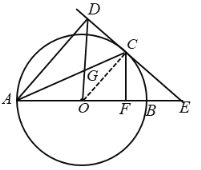
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ∴
∴![]()
∴![]() ∴
∴![]()
由勾股定理![]()
本題考查了圓的有關概念及性質(zhì),切線的性質(zhì),相似三角形的判定與性質(zhì),勾股定理等,解題關鍵是熟練掌握并靈活運用相似三角形的判定與性質(zhì)等.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知:如圖,在四邊形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,點E,F分別是BC,AD的中點.
,點E,F分別是BC,AD的中點.
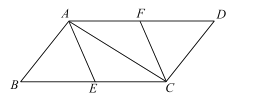
(1)求證:![]() ;
;
(2)當![]() 與
與![]() 滿足什么數(shù)量關系時,四邊形
滿足什么數(shù)量關系時,四邊形![]() 是正方形?請證明.
是正方形?請證明.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小李在景區(qū)銷售一種旅游紀念品,已知每件進價為![]() 元,當銷售單價定為
元,當銷售單價定為![]() 元時,每天可以銷售
元時,每天可以銷售![]() 件.市場調(diào)查反映:銷售單價每提高
件.市場調(diào)查反映:銷售單價每提高![]() 元,日銷量將會減少
元,日銷量將會減少![]() 件,物價部門規(guī)定:銷售單價不能超過
件,物價部門規(guī)定:銷售單價不能超過![]() 元,設銷售單價為
元,設銷售單價為![]() (元).
(元).
(1)要使日銷售利潤為![]() 元,銷售單價應定為多少元;
元,銷售單價應定為多少元;
(2)求日銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元)的函數(shù)關系式,當
(元)的函數(shù)關系式,當![]() 為何值時,日銷售利潤最大,并求出最大利潤.
為何值時,日銷售利潤最大,并求出最大利潤.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】隨著“全民健身”時代的到來,健身已經(jīng)成為推廣文明生活的重要途徑,成為國民增強身體素質(zhì)和提高身體免疫力的重要方法.某校為促進學生對健身知識的了解,在七、八年級中開展了“健身知識知多少”的競賽活動.現(xiàn)從該校七、八年級中各隨機抽取![]() 名學生的競賽成績進行整理描述和分析,下面給出了部分信息:
名學生的競賽成績進行整理描述和分析,下面給出了部分信息:
a.七年級![]() 名學生成績?yōu)椋?/span>
名學生成績?yōu)椋?/span>
![]()
![]()
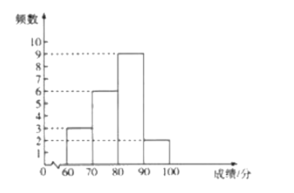
b.八年級![]() 名學生成績的頻數(shù)分布直方圖如圖:
名學生成績的頻數(shù)分布直方圖如圖:
c.八年級成績在![]() 這一組的是:
這一組的是:
![]()
d.七、八年級成績的平均數(shù)、中位數(shù)、眾數(shù)如下:
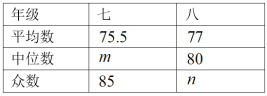
根據(jù)以上信息,回答下列問題:
(1)表中![]() , .
, .
(2)一名七年級學生和一名八年級學生發(fā)生了爭論.均認為本年級的成績更好.請你寫出他們的理由:
七年級學生理由: ;
八年級學生理由: ;
(3)若該校七、八年級各有![]() 名學生.請估計該校七、八年級此次競賽成績優(yōu)秀
名學生.請估計該校七、八年級此次競賽成績優(yōu)秀![]() 的學生共有多少人.
的學生共有多少人.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC和△ABD都是⊙O的內(nèi)接三角形,圓心O在邊AB上,邊AD分別與BC,OC交于E,F兩點,點C為![]() 的中點.
的中點.
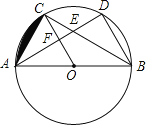
(1)求證:OF∥BD;
(2)若![]() ,且⊙O的半徑R=6cm.①求證:點F為線段OC的中點; ②求圖中陰影部分(弓形)的面積.
,且⊙O的半徑R=6cm.①求證:點F為線段OC的中點; ②求圖中陰影部分(弓形)的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
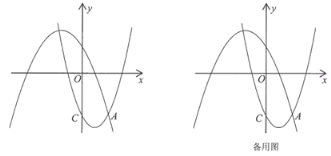
【題目】如圖,在平面直角坐標系xOy中,拋物線L1:![]() 過點C(0,﹣3),與拋物線L2:
過點C(0,﹣3),與拋物線L2:![]() 的一個交點為A,且點A的橫坐標為2,點P、Q分別是拋物線L1、拋物線L2上的動點.
的一個交點為A,且點A的橫坐標為2,點P、Q分別是拋物線L1、拋物線L2上的動點.
(1)求拋物線L1對應的函數(shù)表達式;
(2)若以點A、C、P、Q為頂點的四邊形恰為平行四邊形,求出點P的坐標;
(3)設點R為拋物線L1上另一個動點,且CA平分∠PCR,若OQ∥PR,求出點Q的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
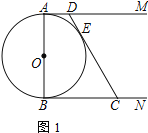
【題目】已知![]() 是
是![]() 的直徑,
的直徑,![]() 和
和![]() 是
是![]() 的兩條切線,
的兩條切線,![]() 與
與![]() 相切于點
相切于點![]() ,分別交
,分別交![]() 、
、![]() 于
于![]() 、
、![]() 兩點
兩點
(1)如圖1,求證:![]()
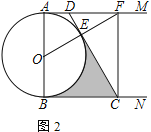
(2)如圖2,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() .若
.若![]() ,
,![]() ,求圖中陰影部分的面積
,求圖中陰影部分的面積
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù) y=ax2+bx+c,其中 y 與 x 的部分對應值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列結(jié)論正確的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 時,y>0D.方程 ax2+bx+c=5 的解為 x1=-2,x2=3
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com