
【題目】閱讀下列材料,并完成相應任務.
 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 折疊,使
折疊,使![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

任務:(1)試根據以上操作步驟證明![]() 就是
就是![]() 的黃金分割點;
的黃金分割點;
(2)請寫出一個生活中應用黃金分割的實際例子.
 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖是計算機中“掃雷”游戲的畫面.在一個有 9×9 個方格的正方形雷區中,隨機埋藏著10顆地雷,每個方格內最多只能藏1顆地雷.小王在游戲開始時隨機地點擊一個方格,點擊后出現了如圖所示的情況.我們把與標號3的方格相鄰的方格記為A區域(畫線部分),A區域外的部分記為B區域.數字3表示在A區域有3顆地雷.為了最大限 度的避開地雷,下一步應該點擊的區域是___. (填“A”或“B”)
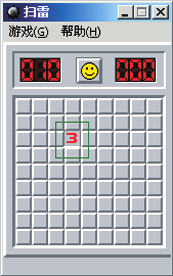
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進一批單價為8元的商品,如果按每件10元出售,那么每天可銷售100件,經調查發現,這種商品的銷售單價每提高1元,其銷售量相應減少10件.
(1)求銷售量![]() 件與銷售單價
件與銷售單價![]() 元之間的關系式;
元之間的關系式;
(2)當銷售單價![]() 定為多少,才能使每天所獲銷售利潤最大?最大利潤是多少?
定為多少,才能使每天所獲銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,且
,且![]() .
.
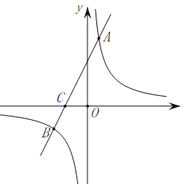
(1)求該反比例函數和一次函數的解析式;
(2)求點![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 有最大值,如果存在,請求出點
有最大值,如果存在,請求出點![]() 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電視臺的一檔娛樂性節目中,在游戲PK環節,為了隨機分選游戲雙方的組員,主持人設計了以下游戲:用不透明的白布包住三根顏色長短相同的細繩AA1、BB1、CC1,只露出它們的頭和尾(如圖所示),由甲、乙兩位嘉賓分別從白布兩端各選一根細繩,并拉出,若兩人選中同一根細繩,則兩人同隊,否則互為反方隊員.
(1)若甲嘉賓從中任意選擇一根細繩拉出,求他恰好抽出細繩AA1的概率;
(2)請用畫樹狀圖法或列表法,求甲、乙兩位嘉賓能分為同隊的概率.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并完成相應任務.
 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 折疊,使
折疊,使![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.
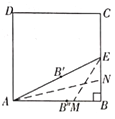
 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 折疊,使
折疊,使![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

任務:(1)試根據以上操作步驟證明![]() 就是
就是![]() 的黃金分割點;
的黃金分割點;
(2)請寫出一個生活中應用黃金分割的實際例子.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,熱氣球的探測器顯示,從熱氣球A看一棟大樓頂部B的俯角為![]() ,看這棟大樓底部C的俯角為
,看這棟大樓底部C的俯角為![]() ,熱氣球A的高度為270米,則這棟大樓的高度為______米
,熱氣球A的高度為270米,則這棟大樓的高度為______米![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的面積為
的面積為![]() ,它的兩條對角線交于點
,它的兩條對角線交于點![]() ,以
,以![]() 、
、![]() 為兩鄰邊作平行四邊形
為兩鄰邊作平行四邊形![]() ,平行四邊形
,平行四邊形![]() 的對角線交于點
的對角線交于點![]() ,同樣以
,同樣以![]() 、
、![]() 為兩鄰邊作平行四邊形
為兩鄰邊作平行四邊形![]() ,…,依此類推,則平行四邊形
,…,依此類推,則平行四邊形![]() 的面積為( )
的面積為( )
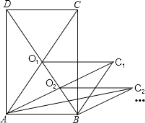
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
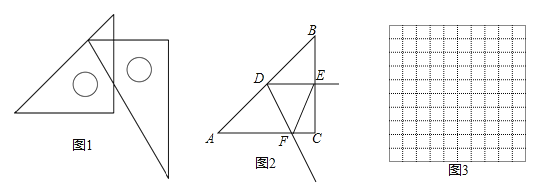
【題目】在數學活動課上,老師提出了一個問題:把一副三角尺如圖擺放,直角三角尺的兩條直角邊分別垂直或平行,60°角的頂點在另一個三角尺的斜邊上移動,在這個運動過程中,有哪些變量,能研究它們之間的關系嗎?
小林選擇了其中一對變量,根據學習函數的經驗,對它們之間的關系進行了探究.
下面是小林的探究過程,請補充完整:
(1)畫出幾何圖形,明確條件和探究對象;
如圖2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是線段AB上一動點,射線DE⊥BC于點E,∠EDF=60°,射線DF與射線AC交于點F.設B,E兩點間的距離為xcm,E,F兩點間的距離為ycm.
(2)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(說明:補全表格時相關數據保留一位小數)
(3)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;
(4)結合畫出的函數圖象,解決問題:當△DEF為等邊三角形時,BE的長度約為 cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com