
【題目】如圖:在數軸上![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,
,![]() 是最大的負整數,且
是最大的負整數,且![]() 滿足
滿足![]() 與
與![]() 互為相反數.
互為相反數.
![]()
(1)![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)若將數軸折疊,使得![]() 點與
點與![]() 點重合,則點
點重合,則點![]() 與數_________表示的點重合;
與數_________表示的點重合;
(3)點![]() 、
、![]() 、
、![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒2個單位長度的速度向左運動,同時,點
以每秒2個單位長度的速度向左運動,同時,點![]() 和點
和點![]() 分別以每秒1個單位長度和3個單位長度的速度向右運動,假設
分別以每秒1個單位長度和3個單位長度的速度向右運動,假設![]() 秒鐘過后,若點
秒鐘過后,若點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,請問:
,請問:![]() 的值是否隨著時間
的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
【答案】(1)![]() ,
,![]() ,
,![]() ;
;
(2)3;
(3)![]() ,不隨著時間
,不隨著時間![]() 的變化而改變;
的變化而改變;
【解析】
(1)根據題意直接求值;(2)由于數軸對折后,對折的點是兩個點的中點,即可求解;(3)點A以每秒2個單位長度的速度向左運動,運動后對應的點為-3-2t;點B以每秒1個單位長度速度向右運動,運動后對應的點為-1+t;點C以每秒3個單位長度速度向右運動,運動后對應的點為5+3t;AB=2+3t, BC=2t+6;![]() ,不隨著時間
,不隨著時間![]() 的變化而改變;
的變化而改變;
解:
(1)∵![]() 與
與![]() 互為相反數,
互為相反數,
∴![]() =0,
=0,![]() =0,
=0,
即a=-3,c=5,
又∵![]() 是最大的負整數,
是最大的負整數,
∴b=-1,
故答案為:a=-3,b=-1,c=5;
(2)由(1)可知,A點表示3,B點表示1,C點表示5,
∵A點與C點重合,
∴對折的點為1,
∴B對折后的點為3;
故答案為:3.
(3)∵點A以每秒2個單位長度的速度向左運動,
∴A運動后對應的點為-3-2t;
∵點B以每秒1個單位長度速度向右運動,
∴B運動后對應的點為-1+t;
∵點C以每秒3個單位長度速度向右運動,
∴運動后對應的點為5+3t;
即AB=2+3t, BC=2t+6;
∵![]() ,
,
∴![]() 的值不隨著時間
的值不隨著時間![]() 的變化而改變;
的變化而改變;


 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:初中數學 來源: 題型:
【題目】如圖![]() ,在矩形紙片
,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() .過點
.過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() ,
,![]() 也隨之移動.
也隨之移動.
①當點![]() 與點
與點![]() 重合時(如圖
重合時(如圖![]() ),求菱形
),求菱形![]() 的邊長;
的邊長;
②若限定![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上移動,求出點
上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形是矩形紙片,AB=2.對折矩形紙片ABCD,使AD與BC重合,折痕為EF;展平后再過點B折疊矩形紙片,使點A落在EF上的點N,折痕BM與EF相交于點Q再次展平,連接BN,MN,延長MN交BC于點G.有如下結論:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等邊三角形;⑤P為線段BM上一動點,H是BN的中點,則PN+PH的最小值是
;④△BMG是等邊三角形;⑤P為線段BM上一動點,H是BN的中點,則PN+PH的最小值是![]() .其中正確結論的序號是___________.
.其中正確結論的序號是___________.
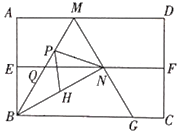
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2014四川資陽)如圖①,已知直線l1∥l2,線段AB在直線l1上,BC垂直于l1交l2于點C,且AB=BC,P是線段BC上異于兩端點的一點,過點P的直線分別交l2,l1于點D,E(點A,E位于點B的兩側,滿足BP=BE,連接AP,CE.
(1)求證:△ABP≌△CBE.
(2)連接AD、BD,BD與AP相交于點F,如圖②.
①當![]() 時,求證:AP⊥BD;
時,求證:AP⊥BD;
②當![]() (n>1)時,設△PAD的面積為S1,△PCE的面積為S2,求
(n>1)時,設△PAD的面積為S1,△PCE的面積為S2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的對角線交于O點,點E,F分別是AO,CO的中點,連接BE,BF,DE,DF,則下列結論中一定成立的是________.(把所有正確結論的序號都填在橫線上)
①BF=DE;②∠ABO=2∠ABE;③S△AED=![]() S△ACD;④四邊形BFDE是菱形.
S△ACD;④四邊形BFDE是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店因換季將某種服裝打折銷售,每件服裝如果按標價的4折出售將虧40元,而按標價8折出售將賺40元.問:
(1)每件服裝的標價是多少元?
(2)每件服裝的成本是多少元?
(3)為了保證不虧損,最多可以打幾折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:在ABCD中,E、F分別是AD、BC邊的中點,G、H是對角線BD上的兩點,且BG=DH,則下列結論中不正確的是( )
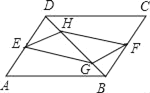
A. GF⊥FHB. GF=EH
C. EF與AC互相平分D. EG=FH
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將四張邊長各不相同的正方形紙片按如圖方式放入矩形ABCD內(相鄰紙片之間互不重疊也無縫隙),未被四張正方形紙片覆蓋的部分用陰影表示,設右上角與左下角陰影部分的周長的差為l.若知道l的值,則不需要測量就能知道周長的正方形的標號為( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數![]() 與反比例函數
與反比例函數![]() .
.
(1)證明:直線與雙曲線沒有交點;
(2)若將直線![]() 向上平移4個單位后與雙曲線恰好有且只有一個交點,求反比例函數的表達式和平移后的直線表達式;
向上平移4個單位后與雙曲線恰好有且只有一個交點,求反比例函數的表達式和平移后的直線表達式;
(3)將(2)小題平移后的直線代表的函數記為![]() ,根據圖象直接寫出:對于負實數
,根據圖象直接寫出:對于負實數![]() ,當
,當![]() 取何值時
取何值時![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com