
【題目】拋物線y=ax2+bx+c的對稱軸為直線x=﹣1,圖象過(1,0)點,部分圖象如圖所示,下列判斷中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若點(﹣0.5,y1),(﹣2,y2)均在拋物線上,則y1>y2;⑤5a﹣2b+c<0.其中正確的個數有( )
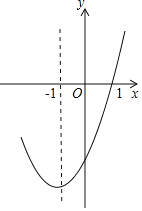
A. 2B. 3C. 4D. 5
【答案】B
【解析】
根據拋物線的開口方向可確定a的符號,再結合對稱軸可確定b的符號,與y軸的交點可確定c的符號,由此可對①進行判斷;由拋物線與x軸交點的個數判定②;根據x=-3時,二次函數的值對③進行判斷;根據拋物線的性質可判斷④;結合b、c和a的數量關系代入可判斷⑤.
∵拋物線開口向上,與y軸交點在x軸下方,
∴a>0,c<0,
∵拋物線對稱軸x=﹣1,經過(1,0),
∴﹣![]() =﹣1,a+b+c=0,
=﹣1,a+b+c=0,
∴b=2a,c=﹣3a,
∴b>0,
∴abc<0,故①錯誤;
∵拋物線與x軸有兩個交點,
∴b2﹣4ac>0,故②正確,
∵拋物線對稱軸x=﹣1,經過(1,0),
∴拋物線與x軸的另一個交點為(﹣3,0),
∴9a﹣3b+c=0,故③正確,
∵點(﹣0.5,y1),(﹣2,y2)均在拋物線上,
﹣1.5>﹣2,
則y1<y2,故④錯誤;
∵5a﹣2b+c=5a﹣4a﹣3a=﹣2a<0,故⑤正確,
故選B.


科目:初中數學 來源: 題型:
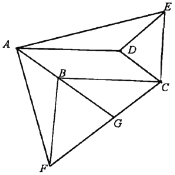
【題目】如圖,在口ABCD中,分別以邊BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,連接AF,AE.
(1)求證:△ABF≌△EDA;
(2)延長AB與CF相交于G,若AF⊥AE,求證BF⊥BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解初三年級1000名學生的身體健康情況,從該年級隨機抽取了若干名學生,將他們按體重(均為整數,單位:kg)分成五組(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依據統計數據繪制了如下兩幅尚不完整的統計圖.

解答下列問題:
(1)這次抽樣調查的樣本容量是 ,并補全頻數分布直方圖;
(2)C組學生的頻率為 ,在扇形統計圖中D組的圓心角是 度;
(3)請你估計該校初三年級體重超過60kg的學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】廣安市紅色旅游資源豐富,無論是小平故里行,還是華鎣山上游,都吸引了不少游客。2014~2018年旅游收入不斷增長,同比增速分別為:17.3%,14.7%,17.3%,16.5%,19.1%,關于這組數據,下列說法正確的是( ).
A. 中位數是14.7%B. 眾數是17.3%
C. 平均數是17.98%D. 方差是0
查看答案和解析>>
科目:初中數學 來源: 題型:
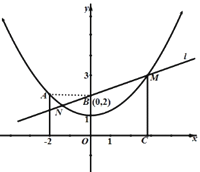
【題目】如圖,已知二次函數y=ax2+1(a≠0,a為實數)的圖象過點A(-2,2),一次函數y=kx+b(k≠0,k、b為實數)的圖象l經過點B(0,2).
(1)求a的值并寫出二次函數表達式;
(2)求b的值;
(3)設直線l與二次函數圖象交于M、N兩點,過M作MC垂直x軸于點C,試證明:MB=MC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是⊙O的內接三角形,AB是⊙O的直徑,OF⊥AB,交AC于點F,點E在AB的延長線上,射線EM經過點C,且∠ACE+∠AFO=180°.
(1)求證:EM是⊙O的切線;
(2)若∠A=∠E,BC=![]() ,求陰影部分的面積.(結果保留
,求陰影部分的面積.(結果保留![]() 和根號).
和根號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,給出如下定義:已知兩個函數,如果對于任意的自變量x,這兩個函數對應的函數值記為y1、y2,恒有點x,y1和點x,y2關于點x,x成中心對稱(此三個點可以重合),由于對稱中心x,x都在直線yx上,所以稱這兩個函數為關于直線yx的“相依函數”.例如:y3x和y5x為關于直線yx的“相依函數”
(1)已知點M1,m是直線y2x4上一點,請求出點M1,m關于點1,1成中心對稱的點N的坐標;
(2)若直線y3xn和它關于直線yx的“相依函數”的圖象與y軸圍成的三角形的面積為8,求n的值;
(3)若二次函數yax2bxc和yx2d為關于直線yx的“相依函數”.
①請求出a、b的值;
②已知點P3,2、點Q2,2,連接PQ,直接寫出yax2bxc和yx2d兩條拋物線與線段PQ有且只有兩個交點時對應的d的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三(1)班部分同學接受一次內容為“最適合自己的考前減壓方式”的調查活動,收集整理數據后,老師將減壓方式分為五類,并繪制了圖1、圖2兩個不完整的統計圖,請根據圖中的信息解答下列問題.
(1)初三(1)班接受調查的同學共有多少名;
(2)補全條形統計圖,并計算扇形統計圖中的“體育活動C”所對應的圓心角度數;
(3)若喜歡“交流談心”的5名同學中有三名男生和兩名女生;老師想從5名同學中任選兩名同學進行交流,直接寫出選取的兩名同學都是女生的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A,B兩點的縱坐標分別為7和1,直線AB與y軸所夾銳角為60°.
(1)求線段AB的長;
(2)求經過A,B兩點的反比例函數的解析式.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com