
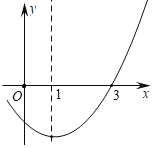
【題目】若二次函數y=x2﹣2x+k的部分圖象如圖所示,則關于x的一元二次方程x2﹣2x+k=0的解一個為x1=3,則方程x2﹣2x+k=0另一個解x2=_____.
【答案】-1
【解析】
利用拋物線與x軸的交點問題,利用關于x的一元二次方程x2-2x+k=0的解一個為x1=3得到二次函數y=x2-2x+k與x軸的一個交點坐標為(3,0),然后利用拋物線的對稱性得到二次函數y=x2-2x+k與x軸的另一個交點坐標為(-1,0),從而得到方程x2-2x+k=0另一個解.
解:∵關于x的一元二次方程x2﹣2x+k=0的解一個為x1=3,
∴二次函數y=x2﹣2x+k與x軸的一個交點坐標為(3,0),
∵拋物線的對稱軸為直線x=1,
∴二次函數y=x2﹣2x+k與x軸的另一個交點坐標為(﹣1,0),
∴方程x2﹣2x+k=0另一個解x2=﹣1.
故答案為﹣1.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,D是AB邊上一點(點D與A,B不重合),連結CD,將線段CD繞點C按逆時針方向旋轉90°得到線段CE,連結BE.
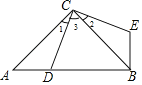
(1)求證:△ACD≌△BCE;
(2)當∠1=25°時,求∠E的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
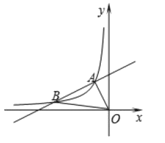
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() 、點
、點![]() ,在
,在![]() 軸上存在一點
軸上存在一點![]() ,使
,使![]() 的周長最小,則點
的周長最小,則點![]() 的坐標是____________________________。
的坐標是____________________________。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某消防隊在一居民樓前進行演習,消防員利用云梯成功救出點B處的求救者后,又發現點B正上方點C處還有一名求救者.在消防車上點A處測得點B和點C的仰角分別是45°和65°,點A距地面2.5米,點B距地面10.5米.為救出點C處的求救者,云梯需要繼續上升的高度BC約為多少米?(結果保留整數.參考數據:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解學生的課外閱讀情況,隨機抽查部分學生,并對其寒假期間的課外閱讀量進行統計分析,繪制成如圖所示但不完整的統計圖.已知抽查的學生在寒假期間閱讀量為2本的人數占抽查總人數的![]() ,根據所給出信息,解答下列問題:
,根據所給出信息,解答下列問題:
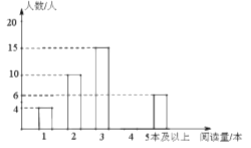
(1)求被抽查學生人數;
(2)將條形統計圖補充完整;
(3)若規定:假期閱讀3本及3本以上課外書者為完成假期作業,據此估計該校1800名學生中,完成假期作業的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() (
(![]() ,
,![]() )的頂點是
)的頂點是![]() ,拋物線
,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,與直線
,與直線![]() 交于點
交于點![]() .過點
.過點![]() 作
作![]() 軸于點
軸于點![]() ,平移拋物線
,平移拋物線![]() 使其經過點
使其經過點![]() 、
、![]() 得到拋物線
得到拋物線![]() (
(![]() ),拋物線
),拋物線![]() 與
與![]() 軸的另一個交點為
軸的另一個交點為![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求點
,求點![]() 的坐標
的坐標
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若四邊形![]() 為矩形,
為矩形,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
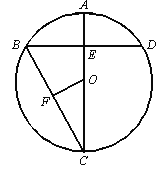
【題目】如圖,AC是⊙O的直徑,弦BD⊥AO于E,連接BC,過點O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半徑;
(2)求O到弦BC的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,AB是![]() 的直徑,C是
的直徑,C是![]() 上一點,連接AC,過點C作直線
上一點,連接AC,過點C作直線![]() 于D(
于D(![]() ),點E是DB上任意一點(點D、B除外),直線CE交
),點E是DB上任意一點(點D、B除外),直線CE交![]() 于點F.連接AF與直線CD交于點G.
于點F.連接AF與直線CD交于點G.
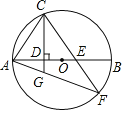
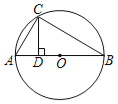
(1)求證:![]()
(2)若點E是AD(點A除外)上任意一點,上述結論是否仍然成立?若成立,請畫出圖形并給予證明;若不成立,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有客房![]() 間供游客居住,當每間客房的定價為每天
間供游客居住,當每間客房的定價為每天![]() 元時,客房恰好全部住滿;如果每間客房每天的定價每增加
元時,客房恰好全部住滿;如果每間客房每天的定價每增加![]() 元,就會減少
元,就會減少![]() 間客房出租.設每間客房每天的定價增加
間客房出租.設每間客房每天的定價增加![]() 元,賓館出租的客房為
元,賓館出租的客房為![]() 間.求:
間.求:
![]() 關于
關于![]() 的函數關系式;
的函數關系式;
![]() 如果某天賓館客房收入
如果某天賓館客房收入![]() 元,那么這天每間客房的價格是多少元?
元,那么這天每間客房的價格是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com