
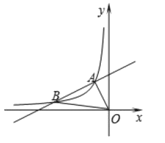
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() 、點
、點![]() ,在
,在![]() 軸上存在一點
軸上存在一點![]() ,使
,使![]() 的周長最小,則點
的周長最小,則點![]() 的坐標是____________________________。
的坐標是____________________________。
【答案】![]()
【解析】
先根據點A求出k2值,再根據反比例函數解析式求出n值,作點A關于x軸的對稱點A′,連接A′B,交x軸于點P,此時△PAB的周長最小,設直線A′B的表達式為y=ax+c,根據待定系數法求得解析式,令y=0,即可求得P的坐標.
(1)∵反比例![]() 的圖象經過點A(-1,2),
的圖象經過點A(-1,2),
∴k2=-1×2=-2,
∴反比例函數表達式為:y=-![]() ,
,
∵反比例y=-![]() 的圖象經過點B(-4,n),
的圖象經過點B(-4,n),
∴-4n=-2,解得n=![]() ,
,
∴B點坐標為(-4,![]() ),
),
如圖,作點A關于x軸的對稱點A′,連接A′B,交x軸于點P,此時△PAB的周長最小,
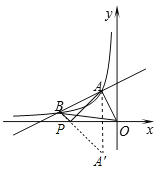
∵點A′和A(-1,2)關于x軸對稱,
∴點A′的坐標為(-1,-2),
設直線A′B的表達式為y=ax+c,
∵經過點A′(-1,-2),點B(-4,![]() )
)
∴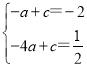 ,
,
解得: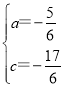 ,
,
∴直線A′B的表達式為:y=-![]() x-
x-![]() ,
,
當y=0時,則x=-![]() ,
,
∴P點坐標為(-![]() ,0).
,0).


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,點O為正方形ABCD的中心,AD=1,BE平分∠DBC交DC于點E,延長BC到點F,使BD=BF,連結DF交BE的延長線于點H,連結OH交DC于點G,連結HC.則以下四個結論中:OH∥BF;②OG:GH=2:1;③GH=![]() ;④∠CHF=2∠EBC;⑤CH2=HEHB.正確結論的個數為( )
;④∠CHF=2∠EBC;⑤CH2=HEHB.正確結論的個數為( )
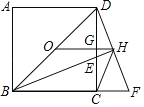
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:線段MN=a.
![]()
(1)求作:邊長為![]() a的正三角形ABC.(要求:尺規(guī)作圖,不寫作法但保留作圖痕跡)
a的正三角形ABC.(要求:尺規(guī)作圖,不寫作法但保留作圖痕跡)
(2)若a=10cm.求(1)中正三角形ABC的內切圓的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
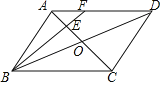
【題目】如圖,在ABCD中,AC,BD相交于點O,點E是OA的中點,連接BE并延長交AD于點F,已知S△AEF=4,則下列結論:①![]() =
=![]() ;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正確的是_____(填序號)
;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正確的是_____(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
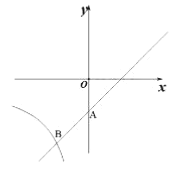
【題目】如圖,在平面直角坐標系中直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與反比例函數在第三象限內的圖象相交于點
,與反比例函數在第三象限內的圖象相交于點![]() 。
。
(1)求反比例函數的關系式;
(2)將直線![]() 沿
沿![]() 軸平移后與反比例函數圖象在第三象限內交于點
軸平移后與反比例函數圖象在第三象限內交于點![]() ,且
,且![]() 的面積為8,求平移后的直線的函數關系式。
的面積為8,求平移后的直線的函數關系式。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一個小球從斜坡的點O處拋出,小球的拋出路線可以用二次函數y=4x﹣![]() x2刻畫,斜坡可以用一次函數y=
x2刻畫,斜坡可以用一次函數y=![]() x刻畫,下列結論錯誤的是( )
x刻畫,下列結論錯誤的是( )

A. 當小球拋出高度達到7.5m時,小球水平距O點水平距離為3m
B. 小球距O點水平距離超過4米呈下降趨勢
C. 小球落地點距O點水平距離為7米
D. 斜坡的坡度為1:2
查看答案和解析>>
科目:初中數學 來源: 題型:
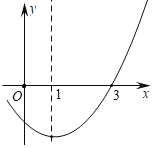
【題目】若二次函數y=x2﹣2x+k的部分圖象如圖所示,則關于x的一元二次方程x2﹣2x+k=0的解一個為x1=3,則方程x2﹣2x+k=0另一個解x2=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】山西省第十五屆運動會乒乓球比賽于2018年8月13日上午在山西省體育博物館的比賽場館內正式拉開了帷幕.第十五屆運動會競技體育組乒乓球項目產生的決賽運動員名單中太原市共27人,其中甲組有甲、乙、丙、丁四名女子運動員,若進行一次乒乓球單打比賽,要通過抽簽從中選出兩名運動員打第一場比賽.
(1)若已確定甲打第一場,再從其余三名運動員中隨機選取一位,求恰好選中乙的概率;
(2)若兩名運動員都不確定,請用樹狀圖法或列表法,求恰好選中甲、乙兩名運動員的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com