
【題目】閱讀材料:如圖1,若點P是⊙O外的一點,線段PO交⊙O于點A,則PA長是點P與⊙O上各點之間的最短距離.
證明:延長PO交⊙O于點B,顯然PB>PA.
如圖2,在⊙O上任取一點C(與點A,B不重合),連結PC,OC.
∵PO<PC+OC,
且PO=PA+OA,OA=OC,
∴PA<PC
∴PA 長是點P與⊙O上各點之間的最短距離.
由此可以得到真命題:圓外一點與圓上各點之間的最短距離是這點到圓心的距離與半徑的差.請用上述真命題解決下列問題.
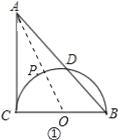
(1)如圖3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC為直徑的半圓交AB于D,P是![]() 上的一個動點,連接AP,則AP長的最小值是 .
上的一個動點,連接AP,則AP長的最小值是 .
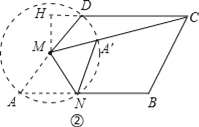
(2)如圖4,在邊長為2的菱形ABCD中,∠A=60°,M是AD邊的中點,點N是AB邊上一動點,將△AMN沿MN所在的直線翻折得到△A′MN,連接A′C,①求線段A’M的長度; ②求線段A′C長的最小值.

【答案】(1)![]() (2)①1②
(2)①1②![]()
【解析】試題分析:(1)由圓外一點與圓上各點之間的最短距離是這點到圓心的距離與半徑的差可得結論;
(2)①利用翻折的性質和菱形的性質可得出結論;
②利用①的結論易得點A′在以點M為圓心,1為半徑的圓上,再利用菱形的性質和銳角三角函數得DH,MH,易得CH,由勾股定理得CM,求得A′C.
解:(1)連接AO與⊙O相交于點P,如圖①,由已知定理可知,
此時AP最短,
∵∠ACB=90°,AC=BC=2,BC為直徑,
∴PO=CO=1,
∴AO=![]() =
=![]() =
=![]() ,
,
∴AP=![]() ﹣1,
﹣1,
故答案為:![]() ﹣1;
﹣1;
(2)①∵將△AMN沿MN所在的直線翻折得到△A′MN,由翻折的性質可得:
A′M=AM,
∵M是AD邊的中點,四邊形ABCD為菱形,邊長為2,
∴AM=1,
∴A′M=1;
②由①知,點A′在以點M為圓心,1為半徑的圓上,
連接CM交圓M于點A′,過點M向CD的延長線作垂線,垂足為點H,如圖②,
∵∠A=60°,四邊形ABCD為菱形,
∴∠HDM=60°,
在Rt△MHD中,
DH=DMcos∠HDM=![]() ,
,
MH=DMsin∠HDM=![]() ,
,
∴CH=CD+DH=2+![]() =
=![]() ,
,
在Rt△CHM中,
CM=![]() =
=![]() =
=![]() ,
,
∴A′C=![]() ﹣1.
﹣1.


科目:初中數學 來源: 題型:
【題目】△CDE和△AOB是兩個等腰直角三角形,∠CDE=∠AOB=90°,DC=DE=1,OA=OB=a(a>1).
(1)將△CDE的頂點D與點O重合,連接AE,BC,取線段BC的中點M,連接OM.
①如圖1,若CD,DE分別與OA,OB邊重合,則線段OM與AE有怎樣的數量關系?請直接寫出你的結果;
②如圖2,若CD在△AOB內部,請你在圖2中畫出完整圖形,判斷OM與AE之間的數量關系是否有變化?寫出你的猜想,并加以證明;
③將△CDE繞點O任意轉動,寫出OM的取值范圍(用含a式子表示);
(2)是否存在邊長最大的△AOB,使△CDE的三個頂點分別在△AOB的三條邊上(都不與頂點重合)?如果存在,請你畫出此時的圖形,并求出邊長a的值;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中, ![]() 為
為![]() 邊上一點,過點
邊上一點,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為折線,將
為折線,將![]() 翻折,設所得的
翻折,設所得的![]() 與梯形
與梯形![]() 重疊部分的面積為
重疊部分的面積為![]() .
.
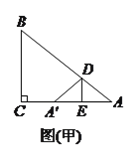
(![]() )如圖(甲),若
)如圖(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,則
,則![]() 的值為__________.
的值為__________.
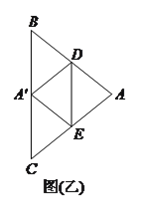
(![]() )如圖(乙),若
)如圖(乙),若![]() ,
, ![]() ,
, ![]() 為
為![]() 中點,則
中點,則![]() 的值為__________.
的值為__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,設
,設![]() .
.
①求![]() 與
與![]() 的函數解析式.
的函數解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若沒有,請說明理由.
的最大值;若沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,每個小正方形的邊長都為1個單位長度,△ABC的三個頂點的位置如圖所示,現將△ABC平移后得△DEF,使點A的對應點為點D,點B的對應點為點E.
(1)畫出△DEF;
(2)連接AD、BE,則線段AD與BE的關系是 ;
(3)求△DEF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地農民一直保持著冬種油菜的習慣,利用農閑冬種一季油菜.該地農業部門對2017年的油菜籽生產成本、市場價格、種植面積和產量等進行了調查統計,并繪制了如下的統計表與統計圖(如圖):
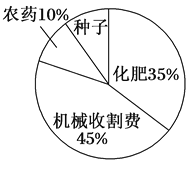
每畝生產成本 | 每畝產量 | 油菜籽市場價格 | 種植面積 |
110元 | 130千克 | 3元/千克 | 500 000畝 |
請根據以上信息解答下列問題:
(1)種植油菜每畝的種子成本是多少元?
(2)農民冬種油菜每畝獲利多少元?
(3)2017年該地全縣農民冬種油菜的總獲利是多少元?(結果用科學記數法表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某餐廳中,一張桌子可坐6人,有如圖所示的兩種擺放方式:

(1)當有n張桌子時,兩種擺放方式各能坐多少人?
(2)一天中午餐廳要接待98位顧客共同就餐,但餐廳只有25張這樣的餐桌.若你是這個餐廳的經理,你打算選擇哪種方式來擺放餐桌?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般情況下![]() 不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得
不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得![]() 成立的一對數a,b為“和諧數對”,記為(a,b).
成立的一對數a,b為“和諧數對”,記為(a,b).
(1)若(3,x)是“和諧數對”,求x的值;
(2)若(m,n)是“和諧數對”,求代數式![]() 的值;
的值;
(3)有一個“和諧數對”(a,b),滿足a-b=1,求a,b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,其頂點坐標為(1,n),且與x軸的一個交點在(3,0)和(4,0)之間,則下列結論:
①ac![]()
②a﹣b+c>0;
③當![]() 時,y隨x的增大而增大
時,y隨x的增大而增大
若(﹣![]() ,y1),(
,y1),(![]() ,y2)是拋物線上的兩點,則y1
,y2)是拋物線上的兩點,則y1![]() y2;
y2;
④一元二次方程ax2+bx+c=n﹣1有兩個不相等的實數根.
其中正確結論的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com