
【題目】張華在一次數學活動中,利用“在面積一定的矩形中,正方形的周長最短”的結論,推導出“式子x+ ![]() (x>0)的最小值是2”.其推導方法如下:在面積是1的矩形中設矩形的一邊長為x,則另一邊長是
(x>0)的最小值是2”.其推導方法如下:在面積是1的矩形中設矩形的一邊長為x,則另一邊長是 ![]() ,矩形的周長是2(x+
,矩形的周長是2(x+ ![]() );當矩形成為正方形時,就有x=
);當矩形成為正方形時,就有x= ![]() (x>0),解得x=1,這時矩形的周長2(x+
(x>0),解得x=1,這時矩形的周長2(x+ ![]() )=4最小,因此x+
)=4最小,因此x+ ![]() (x>0)的最小值是2.模仿張華的推導,你求得式子
(x>0)的最小值是2.模仿張華的推導,你求得式子 ![]() (x>0)的最小值是( )
(x>0)的最小值是( )
A.2
B.1
C.6
D.10
【答案】C
【解析】解:∵x>0, ∴在原式中分母分子同除以x,
即 ![]() =x+
=x+ ![]() ,
,
在面積是9的矩形中設矩形的一邊長為x,則另一邊長是 ![]() ,
,
矩形的周長是2(x+ ![]() );
);
當矩形成為正方形時,就有x= ![]() ,(x>0),
,(x>0),
解得x=3,
這時矩形的周長2(x+ ![]() )=12最小,
)=12最小,
因此x+ ![]() (x>0)的最小值是6.
(x>0)的最小值是6.
故選:C
【考點精析】利用分式的混合運算和完全平方公式對題目進行判斷即可得到答案,需要熟知運算的順序:第一級運算是加法和減法;第二級運算是乘法和除法;第三級運算是乘方.如果一個式子里含有幾級運算,那么先做第三級運算,再作第二級運算,最后再做第一級運算;如果有括號先做括號里面的運算.如順口溜:"先三后二再做一,有了括號先做里."當有多層括號時,先算括號內的運算,從里向外{[(?)]};首平方又末平方,二倍首末在中央.和的平方加再加,先減后加差平方.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,DE⊥AD,交AB于點E,AE為⊙O的直徑 
(1)判斷BC與⊙O的位置關系,并證明你的結論;
(2)求證:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形邊長都是1.請同學們利用網格線進行畫圖:
(1)在圖1中,畫一個頂點為格點、面積為5的正方形;
(2)在圖2中,已知線段AB、CD,畫線段EF,使它與AB、CD組成軸對稱圖形;(要求畫出所有符合題意的線段)
(3)在圖3中,找一格點D,滿足:①到CB、CA的距離相等;②到點A、C的距離相等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以O為坐標原點在正方形網格中建立直角坐標系,若每個小正方形的邊長都為1,網格中有一個格點△ABC(即三角形的頂點都在格點上).
(1)試在y軸上找一點P,使PC+PB的值最小,請在圖中標出P點的位置(留下作圖痕跡),并求出PC+PB的最小值;
(2)將△ABC先向下平移3個單位,再向右平移4個單位后得到△A1B1C1,請在圖中畫出△A1B1C1,并寫出點A1的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,A(-1,0),B(1,0),C(0,1),點D為x軸正半軸上的一個動點,點E為第一象限內一點,且CE⊥CD,CE=CD.
(1)試說明:∠EBC=∠CAB ;
(2)取DE的中點F,連接OF,試判斷OF與AC的位置關系,并說明理由;
(3)在(2)的條件下,試探索O、D、F三點能否構成等腰三角形,若能,請直接寫出所有符合條件的點D的坐標;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD是∠BAC的平分線.若P,Q分別是AD和AC上的動點,則PC+PQ的最小值是( )
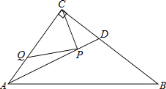
A. 2.4 B. 4.8 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在等腰梯形ABCD中,∠B=60°,P、Q同時從B出發,以每秒1個單位長度分別沿B→A→D→C和B→C→D方向運動至相遇時停止.設運動時間為t(秒),△BPQ的面積為S(平方單位),S與t的函數圖象如圖2,則下列結論錯誤的是( )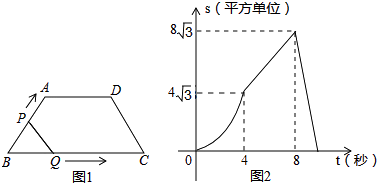
A.當t=4秒時,S=4 ![]()
B.AD=4
C.當4≤t≤8時,S=2 ![]() t
t
D.當t=9秒時,BP平分梯形ABCD的面積
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com