
【題目】若數a使關于x的不等式組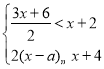 的解集為x<﹣2,且使關于y的分式方
的解集為x<﹣2,且使關于y的分式方![]() 的解為負數,則符合條件的所有整數a的個數為( )
的解為負數,則符合條件的所有整數a的個數為( )
A.4B.5C.6D.7
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在“自主互助學習型課堂競賽”中,為獎勵表現突出的同學,初一(7)班利用班費![]() 元錢,購買鋼筆、相冊、筆記本三種獎品,其中鋼筆至多買
元錢,購買鋼筆、相冊、筆記本三種獎品,其中鋼筆至多買![]() 支,若鋼筆每支
支,若鋼筆每支![]() 元,相冊每本
元,相冊每本![]() 元,筆記本每本
元,筆記本每本![]() 元,在把錢都用盡的條件下,買法共有( )
元,在把錢都用盡的條件下,買法共有( )
A.![]() 種B.
種B.![]() 種C.
種C.![]() 種D.
種D.![]() 種
種
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在抗擊新冠狀病毒戰斗中,有152箱公共衛生防護用品要運到![]() 、
、![]() 兩城鎮,若用大小貨車共15輛,則恰好能一次性運完這批防護用品,已知這兩種大小貨車的載貨能力分別為12箱/輛和8箱/輛,其中用大貨車運往
兩城鎮,若用大小貨車共15輛,則恰好能一次性運完這批防護用品,已知這兩種大小貨車的載貨能力分別為12箱/輛和8箱/輛,其中用大貨車運往![]() 、
、![]() 兩城鎮的運費分別為每輛800元和900元,用小貨車運往
兩城鎮的運費分別為每輛800元和900元,用小貨車運往![]() 、
、![]() 兩城鎮的運費分別為每輛400元和600元.
兩城鎮的運費分別為每輛400元和600元.
(1)求這15輛車中大小貨車各多少輛?
(2)現安排其中10輛貨車前往![]() 城鎮,其余貨車前往
城鎮,其余貨車前往![]() 城鎮,設前往
城鎮,設前往![]() 城鎮的大貨車為
城鎮的大貨車為![]() 輛,前往
輛,前往![]() 、
、![]() 兩城鎮總費用為
兩城鎮總費用為![]() 元,試求出
元,試求出![]() 與
與![]() 的函數解析式.若運往
的函數解析式.若運往![]() 城鎮的防護用品不能少于100箱,請你寫出符合要求的最少費用.
城鎮的防護用品不能少于100箱,請你寫出符合要求的最少費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
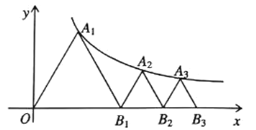
【題目】如圖,已知等邊三角形![]() ,頂點
,頂點![]() 在雙曲線
在雙曲線![]() 上,點
上,點![]() 的坐標為
的坐標為![]() .過
.過![]() 作
作![]() 交雙曲線于點
交雙曲線于點![]() ,過
,過![]() 作
作![]()
![]() 交
交![]() 軸于點
軸于點![]() ,得到第二個等邊
,得到第二個等邊![]() ;過
;過![]() 作
作![]() 交雙曲線于點
交雙曲線于點![]() ,過
,過![]() 作
作![]() 交
交![]() 軸于點
軸于點![]() ,得到第三個等邊
,得到第三個等邊![]() ;以此類推,... 則點
;以此類推,... 則點![]() 的坐標為____.
的坐標為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題)用n個2×1矩形,鑲嵌一個2×n矩形,有多少種不同的鑲嵌方案?(2×n矩形表示矩形的鄰邊是2和n)
(探究)不妨假設有an種不同的鑲嵌方案.為探究an的變化規律,我們采取一般問題特殊化的策略,先從最簡單情形入手,再逐次遞進,最后猜想得出結論.
探究一:用1個2×1矩形,鑲嵌一個2×1矩形,有多少種不同的鑲嵌方案?
如圖(1),顯然只有1種鑲嵌方案.所以,a1=1.
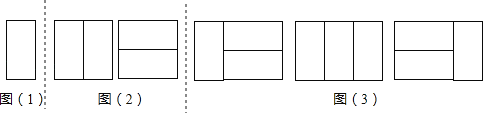
探究二:用2個2×1矩形,鑲嵌一個2×2矩形,有多少種不同的鑲嵌方案?
如圖(2),顯然只有2種鑲嵌方案.所以,a2=2.
探究三:用3個2×1矩形,鑲嵌一個2×3矩形,有多少種不同的鑲嵌方案?
一類:在探究一每個鑲嵌圖的右側再橫著鑲嵌2個2×1矩形,有1種鑲嵌方案;
二類:在探究二每個鑲嵌圖的右側再豎著鑲嵌1個2×1矩形,有2種鑲嵌方案;
如圖(3).所以,a3=1+2=3.
探究四:用4個2×1矩形,鑲嵌一個2×4矩形,有多少種不同的鑲嵌方案?
一類:在探究二每個鑲嵌圖的右側再橫著鑲嵌2個2×1矩形,有 種鑲嵌方案;
二類:在探究三每個鑲嵌圖的右側再豎著鑲嵌1個2×1矩形,有 種鑲嵌方案;
所以,a4= .
探究五:用5個2×1矩形,鑲嵌一個2×5矩形,有多少種不同的鑲嵌方案?
(仿照上述方法,寫出探究過程,不用畫圖)
……
(結論)用n個2×1矩形,鑲嵌一個2×n矩形,有多少種不同的鑲嵌方案?
(直接寫出an與an﹣1,an﹣2的關系式,不寫解答過程).
(應用)用10個2×1矩形,鑲嵌一個2×10矩形,有 種不同的鑲嵌方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市教委為了讓廣大青少年學生走向操場、走進自然、走到陽光下,積極參加體育鍛煉,啟動了“學生陽光體育運動”,其中有一項是短跑運動,短跑運動可以鍛煉人的靈活性,增強人的爆發力,因此張明和李亮在課外活動中報名參加了百米訓練小組.在近幾次百米訓練中,教練對他們兩人的測試成績進行了統計和分析,請根據圖表中的信息解答以下問題:
成績統計分析表
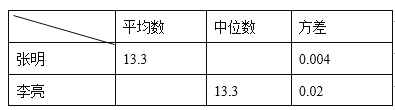
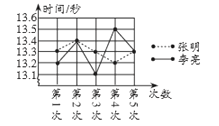
(1)張明第2次的成績為__________秒;
(2)請補充完整上面的成績統計分析表;
(3)現在從張明和李亮中選擇一名成績優秀的去參加比賽,若你是他們的教練,應該選擇誰? 請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個等腰直角三角形放在平面直角坐標系中,∠ACB=90°,點C(-1,0),點B在反比例函數![]() 的圖像上,且y軸平分∠BAC,則k的值是_________.
的圖像上,且y軸平分∠BAC,則k的值是_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求證:無論![]() 為任何實數,此方程總有兩個實數根;
為任何實數,此方程總有兩個實數根;
(2)若方程的兩個實數根為![]() 、
、![]() ,滿足
,滿足![]() ,求
,求![]() 的值;
的值;
(3)若![]() △
△![]() 的斜邊為5,另外兩條邊的長恰好是方程的兩個根
的斜邊為5,另外兩條邊的長恰好是方程的兩個根![]() 、
、![]() ,求
,求![]()
![]() 的內切圓半徑.
的內切圓半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形 ABCD 中,AB=5,AD=13,點 E 為 BC 上一點,將△ABE沿 AE 折疊,使點 B 落在長方形內點 F 處,連接 DF 且 DF=12.

(1)試說明:△ADF 是直角三角形;
(2)求 BE 的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com