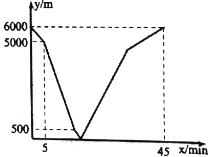
【題目】2019年3月31日，重慶舉行了國際馬拉松比賽，眾多志愿者參與了服務工作，志愿者小茜和小悠分別從“南濱公園”和“朝天門橋”出發，沿同一條筆直的公路相向而行．小茜先出發5分鐘后，小悠立刻騎自行車趕往“南濱公園”．小茜開始騎滑板車，中途改為跑步，且跑步的速度為滑板車速度的一半，到達“朝天門橋”時恰好用了45分鐘．若兩人之間的距離
與小茜離開出發地的時間
之間的關系如圖所示．則當小悠到達“南濱公園”時，小茜離“朝天門橋”的距離為__________米．
科目：初中數學 來源： 題型：
【題目】如圖，已知∠B+∠BCD=180°，∠B=∠D．求證：∠E=∠DFE
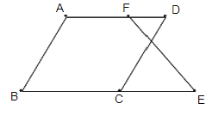
證明：∵∠B+∠BCD=180°（已知）
∴AB∥CD（ ）
∴∠B=∠DCE（ ）
又∵∠B=∠D（已知 ），
∴___________ （等量代換）
∴ ∥
∴∠E=∠DFE（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
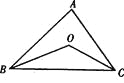
【題目】如圖，在△ ABC中，∠ ABC、∠ ACB的平分線交于點O。
(1)若∠ABC=40°，∠ ACB=50°，則∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°，則∠BOC="________"
(3)若∠A=70°，則∠BOC=_________
(4)若∠BOC=140°，則∠A=________
(5)你能發現∠ BOC與∠ A之間有什么數量關系嗎?寫出并說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
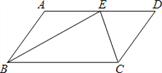
【題目】如圖，在平行四邊形ABCD中，BE、CE分別平分∠ABC、∠BCD，E在AD上，BE =12，CE =5，則平行四邊形ABCD的周長是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：
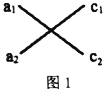
材料一：分解因式是將一個多項式化為若干個整式積的形式的變形，“十字相乘法”可把某些二次三項式分解為兩個一次式的乘積，具體做法如下：對關于
，
的二次三項式
，如圖1，將
項系數
，作為第一列，
項系數
，作為第二列，若
恰好等于
項的系數
，那么可直接分解因式為：
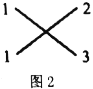
示例1：分解因式：
解：如圖2，其中
，
，而
；
∴
；
示例2：分解因式：
．
解：如圖3，其中，
，而
；
∴
；
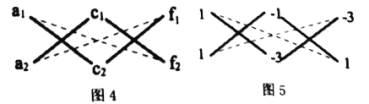
材料二：關于，的二次多項式
也可以用“十字相乘法”分解為兩個一次式的乘積．如圖4，將
作為一列，
作為第二列，
作為第三列，若
，
，
，即第1、2列，第1、3列和第2、3列都滿足十字相乘規則，則原式分解因式的結果為：
；
示例3：分解因式：
．
解：如圖5，其中，
，
；
滿足
，
；
∴
請根據上述材料，完成下列問題：
（1）分解因式：
；
；
（2）若，，
均為整數，且關于，的二次多項式
可用“十字相乘法”分解為兩個一次式的乘積，求出
的值，并求出關于，的方程
的整數解．
查看答案和解析>>
科目：初中數學 來源： 題型：
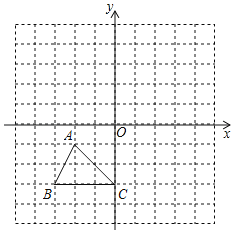
【題目】如圖，把三角形ABC向上平移4個單位長度，再向右平移3個單位長度，得到△A′B′C′．
（1）畫出△A′B′C′；并直接寫出點A′、B′、C′的坐標；
（2）若點P（m，n）是△ABC某邊上的點，經上述平移后，點P的對應點為P′，寫出點P′的坐標（用含m，n的式子表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】教科書中這樣寫道：“我們把多項式
及
叫做完全平方式”，如果一個多項式不是完全平方式，我們常做如下變形：先添加一個適當的項，使式子中出現完全平方式，再減去這個項，使整個式子的值不變，這種方法叫做配方法．配方法是一種重要的解決問題的數學方法，不僅可以將一個看似不能分解的多項式分解因式，還能解決一些與非負數有關的問題或求代數式最大值，最小值等問題．
例如：分解因式
；求代數式
的最小值，
．可知當
時，有最小值，最小值是
，根據閱讀材料用配方法解決下列問題：
（1）分解因式：
_______．
（2）當
為何值時，多項式
有最大值？并求出這個最大值．
（3）利用配方法，嘗試解方程
，并求出
，
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在△ABC中，AB=BC=10，以AB為直徑作⊙O分別交AC，BC于點D，E，連接DE和DB，過點E作EF⊥AB，垂足為F，交BD于點P．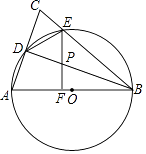
（1）求證：AD=DE；
（2）若CE=2，求線段CD的長；
（3）在（2）的條件下，求△DPE的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
