
【題目】定義:點P(a,b)關于原點的對稱點為P',以PP'為邊作等邊△PP'C,則稱點C為P的“等邊對稱點”;
(1)若P(1,![]() ),求點P的“等邊對稱點”的坐標.
),求點P的“等邊對稱點”的坐標.
(2)若P點是雙曲線y=![]() (x>0)上一動點,當點P的“等邊對稱點”點C在第四象限時,
(x>0)上一動點,當點P的“等邊對稱點”點C在第四象限時,
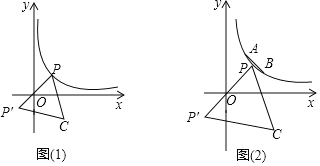
①如圖(1),請問點C是否也會在某一函數圖象上運動?如果是,請求出此函數的解析式;如果不是,請說明理由.
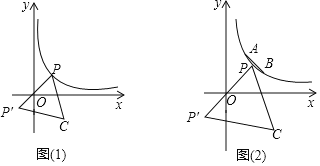
②如圖(2),已知點A(1,2),B(2,1),點G是線段AB上的動點,點F在y軸上,若以A、G、F、C這四個點為頂點的四邊形是平行四邊形時,求點C的縱坐標yc的取值范圍.
【答案】(1)(3,![]() );(2)①是,y=﹣
);(2)①是,y=﹣![]() (x>0);②yc≤﹣6或﹣3<yc≤﹣2
(x>0);②yc≤﹣6或﹣3<yc≤﹣2
【解析】
(1)P(1,![]() )則P'(﹣1,﹣
)則P'(﹣1,﹣![]() ),可求PP'=4;設C(m,n),有PC=P'C=4,通過解方程可得m=﹣
),可求PP'=4;設C(m,n),有PC=P'C=4,通過解方程可得m=﹣![]() n,再進行運算即可;
n,再進行運算即可;
(2)①設P(c,![]() )則P'(﹣c,﹣
)則P'(﹣c,﹣![]() ),可求PP'=2
),可求PP'=2![]() ;設C(s,t),有PC=P'C=2
;設C(s,t),有PC=P'C=2![]() ,通過解方程可得s=﹣
,通過解方程可得s=﹣![]() ,t=
,t=![]() c,令
c,令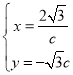 ,消元c即可得xy=﹣6;
,消元c即可得xy=﹣6;
②當AG為平行四邊形的邊時,G與B重合時,為一臨界點通過平移可求得C(1,﹣6),yc≤﹣6;
當AG為平行四邊形的對角線時,G與B重合時,求得C(3,﹣2),G與A重合時,C(2,﹣3),此時﹣3<yc≤﹣2.
解:(1)∵P(1,![]() ),
),
∴P'(﹣1,﹣![]() ),
),
∴PP'=4,
設C(m,n),
∴等邊△PP′C,
∴PC=P'C=4,
∴![]() ,
,
∴m=﹣![]() n,
n,
∴(﹣![]() n﹣1)2+(n﹣
n﹣1)2+(n﹣![]() )2=16.
)2=16.
解得n=![]() 或﹣
或﹣![]() ,
,
∴m=﹣3或m=3.
如圖1,觀察點C位于第四象限,則C(﹣3,![]() ).即點P的“等邊對稱點”的坐標是(3,
).即點P的“等邊對稱點”的坐標是(3,![]() ).
).
(2)①設P(c,![]() ),
),
∴P'(﹣c,﹣![]() ),
),
∴PP'=2![]() ,
,
設C(s,t),
PC=P'C=2![]() ,
,
∴![]() ,
,
∴s=﹣![]() ,
,
∴t2=3c2,
∴t=![]() c,
c,
∴C(﹣![]() ,
,![]() c)或C(
c)或C(![]() ,﹣
,﹣![]() c),
c),
∴點C在第四象限,c>0,
∴C(![]() ,﹣
,﹣![]() c),
c),
令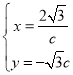 ,
,
∴xy=﹣6,即y=﹣![]() (x>0);
(x>0);
②當AG為平行四邊形的邊時,G與B重合時,為一臨界點通過平移可求得C(1,﹣6),
∴yc≤﹣6;
當AG為平行四邊形的對角線時,G與B重合時,求得C(3,﹣2),
G與A重合時,C(2,﹣3),
此時﹣3<yc≤﹣2,
綜上所述:yc≤﹣6或﹣3<yc≤﹣2.


科目:初中數學 來源: 題型:
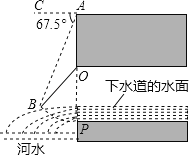
【題目】如圖所示是我國古代城市用以滯洪或分洪系統的局部截面原理圖,圖中OP為下水管道口直徑,OB為可繞轉軸O自由轉動的閥門.平時閥門被管道中排出的水沖開,可排出城市污水;當河水上漲時,閥門會因河水壓迫而關閉,以防河水倒灌入城中.若閥門的直徑OB=OP=100cm,OA為檢修時閥門開啟的位置,且OA=OB.
(1)直接寫出閥門被下水道的水沖開與被河水關閉過程中∠POB的取值范圍;
(2)為了觀測水位,當下水道的水沖開閥門到達OB位置時,在點A處測得俯角∠CAB=67.5°,若此時點B恰好與下水道的水平面齊平,求此時下水道內水的深度.(結果保留小數點后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
科目:初中數學 來源: 題型:
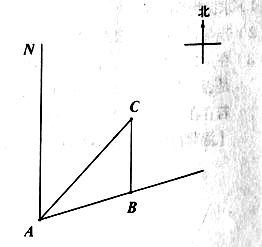
【題目】如圖,一艘船以每小時30海里的速度向北偏東75°方向航行,在點![]() 處測得碼頭
處測得碼頭![]() 的船的東北方向,航行40分鐘后到達
的船的東北方向,航行40分鐘后到達![]() 處,這時碼頭
處,這時碼頭![]() 恰好在船的正北方向,在船不改變航向的情況下,求出船在航行過程中與碼頭
恰好在船的正北方向,在船不改變航向的情況下,求出船在航行過程中與碼頭![]() 的最近距離.(結果精確的0.1海里,參考數據
的最近距離.(結果精確的0.1海里,參考數據![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的頂點B在⊙O上. AC經過圓心0并與圓相交于點D,C,過C作直線CE丄AB,交AB的延長線于點E,且CB平分∠ACE.
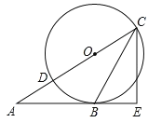
(1)求證:AB是圓O的切線;
(2)若BE=3,CE=4,求圓O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校八年級共400名學生,為了解該年級學生的視力情況,從中隨機抽取40名學生的視力數據作為樣本,數據統計如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根據數據繪制了如下的表格和統計圖:
等級 | 視力(x) | 頻數 | 頻率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合計 | 40 | 1 | |
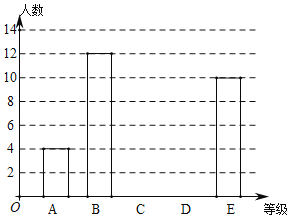
根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)請補全條形統計圖;
(3)根據抽樣調查結果,請估計該校八年級學生視力為“![]() 級”的有多少人?
級”的有多少人?
(4)該年級學生會宣傳部有2名男生和2名女生,現從中隨機挑選2名同學參加“防控近視,愛眼護眼”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
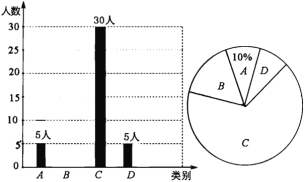
【題目】央視“經典詠流傳”開播以來受到社會廣泛關注.我市某校就“中華文化我傳承——地方戲曲進校園”的喜愛情況進行了隨機調查,對收集的信息進行統計,繪制了下面兩副尚不完整的統計圖.請你根據統計圖所提供的信息解答下列問題:
圖中A表示“很喜歡”,B表示“喜歡”,C表示“一般”,D表示“不喜歡”.
(1)被調查的總人數是_____________人,扇形統計圖中C部分所對應的扇形圓心角的度數為_______.
(2)補全條形統計圖;
(3)若該校共有學生1800人,請根據上述調查結果,估計該校學生中A類有__________人;
(4)在抽取的A類5人中,剛好有3個女生2個男生,從中隨機抽取兩個同學擔任兩角色,用樹形圖或列表法求出被抽到的兩個學生性別相同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,∠BAC=20°,點O是AB的中點,將OB繞點O順時針旋轉α角時(0°<α<180°),得到OP,當△ACP為等腰三角形時,α的值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AD、BD分別是![]() 的內角∠BAC、∠ABC的平分線,過點A作AE⊥AD,交BD的延長線于點E.
的內角∠BAC、∠ABC的平分線,過點A作AE⊥AD,交BD的延長線于點E.

(1)求證:![]() ;
;
(2)如圖2,如果AE=AB,且BD:DE=2:3,求BC:AB的值;
(3)如果∠ABC是銳角,且![]() 與
與![]() 相似,求∠ABC的度數,并直接寫出
相似,求∠ABC的度數,并直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
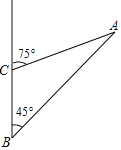
【題目】青白江鳳凰湖濕地公園是一處具有國際水準的旅游度假區,以生態、休閑、水景環境及具有多國風情的建筑為特色.如圖為鳳凰湖濕地公園三個景點A,B,C的平面示意圖,景點C在B的正北方向4千米處,景點A在B的東北方向,在C的北偏東75°方向上,求景點A、B之間的距離.(結果保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com