深爱五月激情网,国模私拍在线观看,亚洲av无码专区在线

精英家教網 > 初中數學 > 題目詳情

已知關于x的一元二次方程mx²﹣（m+2）x+2=0．

（1）證明：不論m為何值時，方程總有實數根；

（2）m為何整數時，方程有兩個不相等的正整數根．

解：（1）△=（m+2）²﹣8m

=m²﹣4m+4

=（m﹣2）²，

∵不論m為何值時，（m﹣2）²≥0，

∴△≥0，

∴方程總有實數根；

（2）解方程得，x=，

x₁=，x₂=1，

∵方程有兩個不相等的正整數根，

∴m=1或2，m=2不合題意，

∴m=1．

練習冊系列答案

課課練與單元測試系列答案

世紀金榜小博士單元期末一卷通系列答案

單元測試AB卷臺海出版社系列答案

黃岡新思維培優考王單元加期末卷系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源：2014-2015學年江蘇省濱海縣八年級上學期期末考試數學試卷（解析版） 題型：解答題

(本題10分)如圖，△ABC中，AB＝AC，D、E、F分別在BC、AB、AC上，且BE＝CD，BD＝CF．

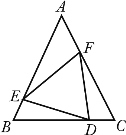
（1）求證：DE＝DF；

（2）當∠A的度數為多少時，△DEF是等邊三角形，并說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

定義：只有一組對角是直角的四邊形叫做損矩形，連接它的兩個非直角頂點的線段叫做這個損矩形的直徑，即損矩形外接圓的直徑．

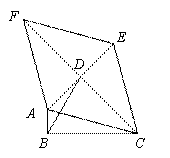
如圖，△ABC中，∠ABC=90º，以AC為一邊向形外作菱形ACEF，點D是菱形ACEF對角線的交點，連接BD，若∠DBC=60º，∠ACB=15º，BD=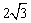，則菱形ACEF的面積為．

查看答案和解析>>

科目：初中數學 來源： 題型：

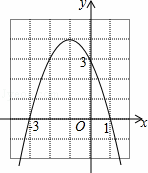
如圖是二次函數y=ax²+bx+c的圖象，下列結論：

①二次三項式ax²+bx+c的最大值為4；

②4a+2b+c＜0；

③一元二次方程ax²+bx+c=1的兩根之和為﹣1；

④使y≤3成立的x的取值范圍是x≥0．

其中正確的個數有（　　）

查看答案和解析>>

科目：初中數學 來源： 題型：

古希臘數學家把數1，3，6，10，15，21，…叫做三角數，它有一定的規律性．若把第一個三角數記為a₁，第二個三角數記為a₂…，第n個三角數記為a_n，計算a₁+a₂，a₂+a₃，a₃+a₄，…由此推算a₃₉₉+a₄₀₀=　

查看答案和解析>>

科目：初中數學 來源： 題型：

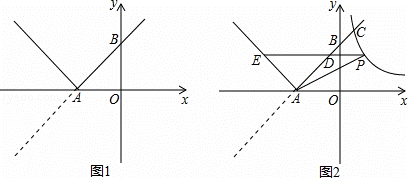
如圖1，已知直線y=x+3與x軸交于點A，與y軸交于點B，將直線在x軸下方的部分沿x軸翻折，得到一個新函數的圖象（圖中的“V形折線”）．

（1）類比研究函數圖象的方法，請列舉新函數的兩條性質，并求新函數的解析式；

（2）如圖2，雙曲線y=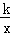與新函數的圖象交于點C（1，a），點D是線段AC上一動點（不包括端點），過點D作x軸的平行線，與新函數圖象交于另一點E，與雙曲線交于點P．

①試求△PAD的面積的最大值；

②探索：在點D運動的過程中，四邊形PAEC能否為平行四邊形？若能，求出此時點D的坐標；若不能，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

如圖，在△ABC中，點D、E分別在邊AB、AC上，下列條件中不能判斷△ABC∽△AED的是（　　）

A．

∠AED=∠B

B．

∠ADE=∠C

C．

D．

查看答案和解析>>

科目：初中數學 來源： 題型：

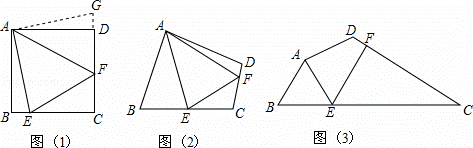
問題：如圖（1），點E、F分別在正方形ABCD的邊BC、CD上，∠EAF=45°，試判斷BE、EF、FD之間的數量關系．

【發現證明】

小聰把△ABE繞點A逆時針旋轉90°至△ADG，從而發現EF=BE+FD，請你利用圖（1）證明上述結論．

【類比引申】

如圖（2），四邊形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，點E、F分別在邊BC、CD上，則當∠EAF與∠BAD滿足　　關系時，仍有EF=BE+FD．

【探究應用】

如圖（3），在某公園的同一水平面上，四條通道圍成四邊形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分別有景點E、F，且AE⊥AD，DF=40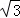（﹣1）米，現要在E、F之間修一條筆直道路，求這條道路EF的長（結果取整數，參考數據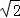：=1.41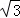，=1.73）