
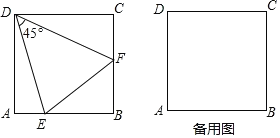
【題目】如圖,在正方形ABCD中,E為直線AB上的動點(不與A,B重合),作射線DE并繞點D逆時針旋轉45°,交直線BC邊于點F,連結EF.
探究:當點E在邊AB上,求證:EF=AE+CF.
應用:(1)當點E在邊AB上,且AD=2時,則△BEF的周長是______.
(2)當點E不在邊AB上時,EF,AE,CF三者的數量關系是______.
【答案】4EF=CF-AE或EF=AE-CF
【解析】
探究:作輔助線,構建全等三角形,證明△DAG≌△DCF(SAS),得∠1=∠3,DG=DF,再證明△GDE≌△FDE(SAS),根據EG的長可得結論;
應用:
(1)利用探究的結論計算三角形周長為4;
(2)分兩種情況:①點E在BA的延長線上時,如圖2,EF=CF-AE,②當點E在AB的延長線上時,如圖3,
EF=AE-CF,兩種情況都是作輔助線,構建全等三角形,證明兩三角形全等得線段相等,根據線段的和與差得出結論.
探究:證明:如圖,延長BA到G,使AG=CF,連接DG,
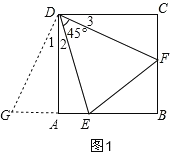
∵四邊形ABCD是正方形,
∴DA=DC,∠DAG=∠DCF=90°,
∴△DAG≌△DCF(SAS),
∴∠1=∠3,DG=DF,
∵∠ADC=90°,∠EDF=45°,
∴∠EDG=∠1+∠2=∠3+∠2=45°=∠EDF,
∵DE=DE,
∴△GDE≌△FDE(SAS),
∴EF=EG=AE+AG=AE+CF;
應用:
(1)△BEF的周長=BE+BF+EF ,
由探究得:EF=AE+CF,
∴△BEF的周長=BE+BF+AE+CF=AB+BC=2+2=4,
故答案為:4;
(2)當點E不在邊AB上時,分兩種情況:
①點E在BA的延長線上時,如圖2,
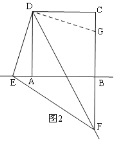
EF=CF-AE,理由是:
在CB上取CG=AE,連接DG,
∵∠DAE=∠DCG=90°,AD=DC,
∴△DAE≌△DCG(SAS)
∴DE=DG,∠EDA=∠GDC
∵∠ADC=90°,
∴∠EDG=90°
∴∠EDF+∠FDG=90°,
∵∠EDF=45°,
∴∠FDG=90°-45°=45°,
∴∠EDF=∠FDG=45°,
在△EDF和△GDF中,
∵DE=DG,∠EDF=∠GDF,DF=DF
∴△EDF≌△GDF(SAS),
∴EF=FG,
∴EF=CF-CG=CF-AE;
②當點E在AB的延長線上時,如圖3,
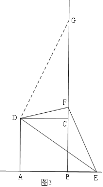
EF=AE-CF,理由是:
延長BC到G,使CG=AE, 連接DG,
∵DA=DC,∠DAE=∠DCG=90°, CG=AE
∴△DAE≌△DCG
∴DE=DG, ∠ADE=∠CDG.
∴∠ADE+∠EDC=∠CDG+∠EDC=90.
即:∠ADC=∠EDG=90,
∵∠EDF=45°,
∴∠GDF=90°-45°=45°,
∴∠EDF=∠GDF,
∵DF=DF,∠EDF=∠GDF,DE=DG
∴△EDF≌△GDF,
∴EF=GF,
∴EF=CG-CF=AE-CF;
綜上所述,當點E不在邊AB上時,EF,AE,CF三者的數量關系是:EF=CF-AE或EF=AE-CF;


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,BD為△ABC的角平分線,且BD=BC,E為BD延長線上的一點,BE=BA,過E作EF⊥AB,F為垂足,下列結論:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正確的是________(填序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解方程:
(1)25 y 2- 16 = 0; (2)y 2+ 2 y-99=0;
(3)3x 2 + 2x -3=0; (4)(2x + 1)2 =3(2x + 1).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在直角坐標系中,
(1)把△ABC向上平移3個單位,再向右平移2個單位得△A′B′C′,在圖中畫出兩次平移后得到的圖形△A′B′C′,并寫出A′、B′、C′的坐標.
(2)如果△ABC內部有一點Q,根據(1)中所述平移方式得到對應點Q′,如果點Q′坐標是(m,n),那么點Q的坐標是_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩地相距60km,甲從A地去B地,乙從B地去A地,圖中![]() 、
、![]() 分別表示甲、乙兩人到B地的距離y(km)與甲出發時間x(h)的函數關系圖象.
分別表示甲、乙兩人到B地的距離y(km)與甲出發時間x(h)的函數關系圖象.
(1)根據圖象,求乙的行駛速度.
(2)解釋交點A的實際意義.
(3)求甲出發多少時間,兩人之間恰好相距5km?


查看答案和解析>>
科目:初中數學 來源: 題型:
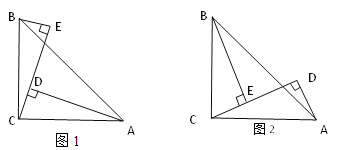
【題目】如圖1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)求證: △BCE≌△CAD;
(2)猜想:AD,DE,BE的數量關系為 (不需證明);
(3)當CE繞點C旋轉到圖2位置時,猜想線段AD,DE,BE之間又有怎樣的數量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=kx+b經過點A(5,0),B(1,4).
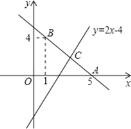
(1)求直線AB的解析式;
(2)若直線y=2x﹣4與直線AB相交于點C,求點C的坐標;
(3)根據圖象,寫出關于x的不等式2x﹣4≥kx+b的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com