【題目】如圖，矩形
的兩條邊
、
分別在
軸和
軸上，已知點
坐標為(4，–3).把矩形沿直線
折疊，使點
落在點
處，直線與、
、
的交點分別為
、
、
.
(1)線段
；
(2)求點坐標及折痕的長;
(3)若點
在軸上，在平面內是否存在點
，使以、、、為頂點的四邊形是菱形?若存在，則請求出點的坐標;若不存在，請說明理由;
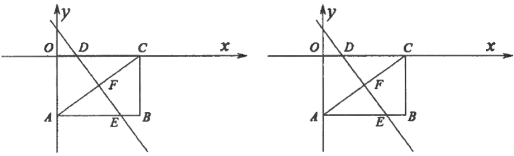
【答案】（1）
；（2）
；拆痕DE的長為
； （3）點Q坐標為
【解析】
（1）根據B點的坐標即可求得AC的長度.
（2）首先根據已知條件證明
，再根據相似比例計算DF、CD的長度
即可計算出D點的坐標，再證明
，根據EF=DF，即可計算的DE的長度.
（3）根據等腰三角形的性質，分類討論第一種情況當
時；第二種情況當
時；第三種情況當
時，分別計算即可.
解：（1）
（2）
，由折疊可得：
,
.
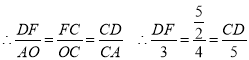∵四邊形OABC是矩形，
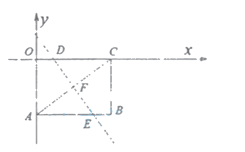
∴拆痕DE的長為
（3）由（2）可知，
，
若以P、D、E、Q為頂點的四邊形是菱形，則
必為等腰三角形。
當時，可知
，
此時PE為對角線，可得
當時，可知
，此時DP為對角線，可得
；
當時，P與C重合，Q與A重合，
綜上所述，滿足條件的點Q坐標為
挑戰100單元檢測試卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，在正方形
中，點
、
是正方形內兩點，
，
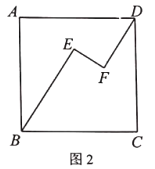
，為探索這個圖形的特殊性質，某數學興趣小組經歷了如下過程：
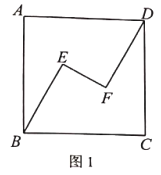
（1）在圖1中，連接
，且
①求證：
與互相平分；
②求證：
；
（2）在圖2中，當
，其它條件不變時，是否成立？若成立，請證明：若不成立，請說明理由.
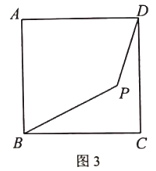
（3）在圖3中，當
，
，
時，求
之長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2﹣4ax+3a．
（Ⅰ）求該二次函數的對稱軸；
（Ⅱ）若該二次函數的圖象開口向下，當1≤x≤4時，y的最大值是2，且當1≤x≤4時，函數圖象的最高點為點P，最低點為點Q，求△OPQ的面積；
（Ⅲ）若對于該拋物線上的兩點P（x1，y1），Q（x2，y2），當t≤x1≤t+1，x2≥5時，均滿足y1≥y2，請結合圖象，直接寫出t的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面是小東設計的“作平行四邊形ABCD，使∠B=45°，AB=2cm,BC=3cm”的作圖過程．
（1）作法：如圖，①畫∠B=45°；
②在∠B的兩邊上分別截取BA=2cm,BC=3cm.
③以點A為圓心，BC長為半徑畫弧，以點
為圓心，AB長為半徑畫弧，兩弧相交于點D；則四邊形ABCD為所求的平行四邊形．
根據小東設計的作圖過程，
（1）使用直尺和圓規，補全圖形；（保留作圖痕跡）
（2）完成下面的證明．
證明：∵
_______，
_______，
∴四邊形ABCD為所求的平行四邊形．（____________）（填推理的依據）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有20筐白菜，以每筐25千克為標準，超過或不足的千克數分別用正、負數來表示，記錄如下：
與標準質量的差值（單位：千克） |
|
|
| 0 | 1 | 2.5 |
筐數 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最輕的一筐多重多少千克？
（2）與標準重量比較，20筐白菜總計超過或不足多少千克？
（3）若白菜每千克售價2.8元，則出售這20筐白菜可賣多少元？（結果保留整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在平面直角坐標系中，點O是坐標原點，四邊形ABCO是菱形，點A的坐標為（﹣3，4），點C在x軸的正半軸上，直線AC交y軸于點M，AB邊交y軸于點H，連接BM.
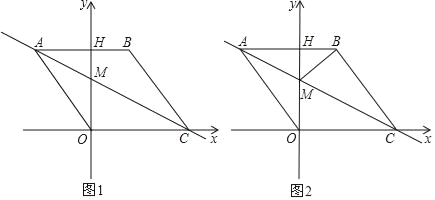
（1）菱形ABCO的邊長
（2）求直線AC的解析式；
（3）動點P從點A出發，沿折線ABC方向以2個單位/秒的速度向終點C勻速運動，設△PMB的面積為S（S≠0），點P的運動時間為t秒，
①當0＜t＜
時，求S與t之間的函數關系式；
②在點P運動過程中，當S=3，請直接寫出t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 要了解某公司生產的100萬只燈泡的使用壽命，可以采用抽樣調查的方法
B. 4位同學的數學期末成績分別為100、95、105、110，則這四位同學數學期末成績的中位數為100
C. 甲乙兩人各自跳遠10次，若他們跳遠成績的平均數相同，甲乙跳遠成績的方差分別為0.51和0.62
D. 某次抽獎活動中，中獎的概率為
表示每抽獎50次就有一次中獎
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】服裝店10月份以每套500元的進價購進一批羽絨服，當月以標價銷售，銷售額14000元，進入11月份搞促銷活動，每件降價50元，這樣銷售額比10月份增加了5500元，售出的件數是10月份的1.5倍．
（1）求每件羽絨服的標價是多少元；
（2）進入12月份，該服裝店決定把剩余的羽絨服按10月份標價的八折銷售，結果全部賣掉，而且這批羽絨服總獲利不少于12700元，問這批羽絨服至少購進多少件？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，二次函數y=ax2+bx+c的圖象開口向上，且經過點A（0，
）．
（1）若此函數的圖象經過點（1，0）、（3，0），求此函數的表達式；
（2）若此函數的圖象經過點B（2，﹣
），且與x軸交于點C、D．
①填空：b=_____（用含α的代數式表示）；
②當CD2的值最小時，求此函數的表達式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
