
(本題滿分12分)在平面直角坐標系中,拋物線C :y=
:y= x
x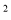 +4x+4
+4x+4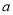 (0<
(0<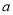 <2),
<2),


(1)當C 與x軸有唯一交點時,求C
與x軸有唯一交點時,求C 的解析式;
的解析式;
(2)若 =1,將拋物線C
=1,將拋物線C 先向右平移2個單位,再向下平移1個單位得拋物線C
先向右平移2個單位,再向下平移1個單位得拋物線C ,拋物線C
,拋物線C 與x軸相交于M、N兩點(M點在N點的左邊),直線y=kx(k>0)與拋物線C
與x軸相交于M、N兩點(M點在N點的左邊),直線y=kx(k>0)與拋物線C 相交于P、Q(P在第三象限)且△NOQ的面積是△MOP的面積的4倍,求k的值;
相交于P、Q(P在第三象限)且△NOQ的面積是△MOP的面積的4倍,求k的值;
(3)若A(1,y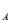 ),B(0,y
),B(0,y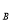 ),C(-1,y
),C(-1,y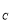 )三點均在C
)三點均在C 上,連BC,作AE∥BC交拋物線C
上,連BC,作AE∥BC交拋物線C 于E,求證:當
于E,求證:當 值變化時,E點在一條直線上.
值變化時,E點在一條直線上.
(1)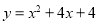 ;(2)
;(2)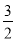 ;(3)證明詳見解析.
;(3)證明詳見解析.
【解析】
試題分析:(1)根據二次函數與一元二次方程的關系,可知 有兩個相等的實數根,據此求出a的值;
有兩個相等的實數根,據此求出a的值;
(2)設P( ,
, ),Q(
),Q( ,
,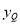 ),得到
),得到 、
、 為方程
為方程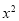 -1=kx的兩根,∴
-1=kx的兩根,∴
 =-1 ∴
=-1 ∴ =-
=- ,
, =2,進而得到k=
=2,進而得到k=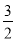 ;
;
(3)作CD⊥y軸于D,作AQ⊥x軸于Q,作EG⊥AQ于G,則△AEG∽△BCD,設E(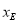 ,
,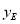 ) ,得到關于
) ,得到關于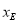 的等式,解得
的等式,解得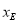 的值,即可得到點E所在的直線關系式.
的值,即可得到點E所在的直線關系式.
試題解析:(1)拋物線C 與x軸有唯一交點,即當y=0時,
與x軸有唯一交點,即當y=0時, 有兩個相等的實數根,此時
有兩個相等的實數根,此時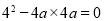 ,解得:a=
,解得:a= ,因為0<
,因為0< <2,所以a=1,所以拋物線C
<2,所以a=1,所以拋物線C 的解析式為
的解析式為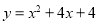 ;
;
(2)設P( ,
, ),Q(
),Q( ,
,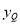 ),則:
),則: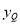 =-4
=-4 ,∴
,∴ =-4
=-4 ,且
,且 、
、 為方程
為方程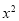 -1=kx的兩根,∴
-1=kx的兩根,∴
 =-1 ∴
=-1 ∴ =-
=- ,
, =2,∴k=
=2,∴k=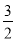 .
.
(3) 作CD⊥y軸于D,作AQ⊥x軸于Q,作EG⊥AQ于G,則△AEG∽△BCD,∴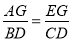 ,設E(
,設E(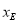 ,
,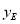 ) ,∴
) ,∴ =a+4+4a ,
=a+4+4a , =4a ,
=4a ,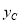 =a-4+4a,
=a-4+4a,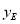 =a
=a +4
+4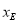 +4a,∴
+4a,∴ ,∵
,∵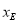 ≠1,∴
≠1,∴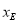 =-2,即E點在直線x=-2上.
=-2,即E點在直線x=-2上.

考點:二次函數與一元二次方程的關系;二次函數的綜合應用.
考點分析: 考點1:二次函數 定義: (a,b,c是常數,a≠0),那么y叫做x 的二次函數。
(a,b,c是常數,a≠0),那么y叫做x 的二次函數。  (a≠0)中x、y是變量,a,b,c是常數,自變量x 的取值范圍是全體實數,b和c可以是任意實數,a是不等于0的實數,因為a=0時,
(a≠0)中x、y是變量,a,b,c是常數,自變量x 的取值范圍是全體實數,b和c可以是任意實數,a是不等于0的實數,因為a=0時, 變為y=bx+c若b≠0,則y=bx+c是一次函數,若b=0,則y=c是一個常數函數。
變為y=bx+c若b≠0,則y=bx+c是一次函數,若b=0,則y=c是一個常數函數。 (a≠0)與一元二次方程
(a≠0)與一元二次方程 (a≠0)有密切聯系,如果將變量y換成一個常數,那么這個二次函數就是一個一元二次函數。
二次函數的解析式有三種形式:
(a≠0)有密切聯系,如果將變量y換成一個常數,那么這個二次函數就是一個一元二次函數。
二次函數的解析式有三種形式:  (a,b,c是常數,a≠0);
(a,b,c是常數,a≠0);  (a,h,k是常數,a≠0)
(a,h,k是常數,a≠0)  與x軸有交點時,即對應二次好方程
與x軸有交點時,即對應二次好方程 有實根x1和x2存在時,根據二次三項式的分解因式
有實根x1和x2存在時,根據二次三項式的分解因式 ,二次函數
,二次函數 可轉化為兩根式
可轉化為兩根式 。如果沒有交點,則不能這樣表示。
。如果沒有交點,則不能這樣表示。  (a≠0)的形式,那么這個函數就是二次函數,否則就不是。
試題屬性
(a≠0)的形式,那么這個函數就是二次函數,否則就不是。
試題屬性


科目:初中數學 來源:2014-2015學年陜西省西安市九年級下學期第一次月考數學試卷(解析版) 題型:選擇題
下列四個點中,在反比例函數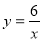 的圖像上的是( )
的圖像上的是( )
A.(1,-6) B.(2,4) C.(3,-2) D.(-6,-1)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市第一教研片九年級下學期第一次月考數學試卷(解析版) 題型:選擇題
一只因損壞而傾斜的椅子,從背后看到的形狀如圖,其中兩組對邊的平行關系沒有發生變化,若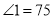 ,則
,則 的大小是( ).
的大小是( ).
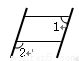
A.75 B.115 C.65 D.105
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省九年級3月聯考數學試卷(解析版) 題型:解答題
(本題滿分8分)為響應我市“中國夢”“武漢夢”主題教育活動,某中學在全校學生中開展了以“中國夢我的夢”為主題的征文比賽,評選出一、二、三等獎和優秀獎.小明同學根據獲獎結果,繪制成如圖所示的統計表和數學統計圖.
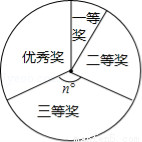

請你根據以上圖表提供的信息,解答下列問題:
(1)a= ,b= ,n= .
(2)學校決定在獲得一等獎的作者中,隨機推薦兩名作者代表學校參加市級比賽,其中王夢、李剛都獲得一等獎,請用畫樹狀圖或列表的方法,求恰好選中這二人的概率.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省九年級3月聯考數學試卷(解析版) 題型:解答題
(本題8分)如圖,在平面直角坐標系中,△ABC的三個頂點都在格點上,點A的坐標為(2,4),請解答下列問題:
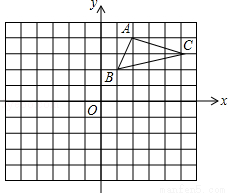
(1)畫出△ABC關于x軸對稱的△A1B1C1,并直接寫出點A1的坐標.(4分)
(2)畫出△A1B1C1繞原點O旋轉180°后得到的△A2B2C2,若△A1B1C1內一點P的坐標為(a,b),請直接寫出點P在△A2B2C2內對應點P′的坐標.(4分)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧省丹東市九年級上學期第一次月考數學試卷(解析版) 題型:解答題
如圖,在ΔABC中,∠ABC=90,BD為AC的中線,過點C作CE⊥BD于點E,過點A作BD的平行線,交CE的延長線于點F,在AF的延長線上截取FG=BD,連接BG、DF
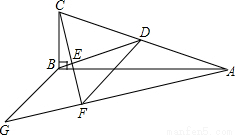
(1)猜想四邊形BDFG的形狀,并說明理由
(2)若AF=8,CF=6,求四邊形BDFG的周長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com