
【題目】4月23日是世界讀書日,設立的目的是推動更多的人去閱讀和寫作.為了解學生的課外閱讀情況,對某校八年級1班“你最喜愛的課外閱讀書目”進行調查(每名學生必須選一類且只能選一類閱讀書目),并根據調查結果繪制成如圖所示的兩幅統計圖(不完整).
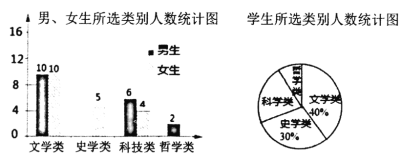
根據以上信息解決下列問題
(1)所抽查的學生中,選史學類的男生有______人,選哲學類的女生有______人;
(2)扇形統計圖中“科學類”所對應扇形圓心角度數為_______°;
(3)若該校有2000名學生,請估計該校喜愛“科學類”的學生共有多少人?
(4)從所抽取的選“哲學類”的學生中,隨機選取兩名學生參加區級辯論賽,請用樹狀圖或列表法求出所選取的兩名學生恰好選中一個男生、一個女生的概率.
【答案】(1)10;3;(2)72;(3)![]() (4)表格見解析;
(4)表格見解析;![]()
【解析】
(1)利用選文學類的人數除以其所占調查人數的百分比即可求出調查人數,然后利用調查人數乘以30%即可求出選史學類的人數,從而計算出選史學類的男生人數,再利用調查人數減去其余各類人數即可求出選哲學類的女生人數;
(2)利用選科學類人數除以調查總人數再乘360°即可求出結論;
(3)利用選科學類人數除以調查總人數再乘2000即可求出結論;
(4)根據題意,列出表格,然后利用概率公式求概率即可.
解:(1)調查總人數為(10+10)÷40%=50人
選史學類的男生有50×30%-5=10人
選哲學類的女生有50-10-10-10-5-6-4-2=3人
故答案為:10;3;
(2)(6+4)÷50×360°=72°
故答案為72;
(3)![]()
![]() (人)
(人)
答:估計該校喜愛“科學類”的學生共有400人;
(4)列表如下:
男1 | 男2 | 女1 | 女2 | 女3 | |
男1 | 男2,男1 | 女1,男1 | 女2,男1 | 女3,男1 | |
男2 | 男1,男2 | 女1,男2 | 女2,男2 | 女3,男2 | |
女1 | 男1,女1 | 男2,女1 | 女2,女/span>1 | 女3,女1 | |
女2 | 男1,女2 | 男2,女2 | 女1,女2 | 女3,女2 | |
女3 | 男1,女3 | 男2,女3 | 女1,女3 | 女2,女3 |
由表格可知:共有20種等可能的結果,其中所選取的兩名學生恰好選中一個男生、一個女生的可能有12種,
![]()
答:所選取的兩名學生恰好選中一個男生、一個女生的概率為![]() .
.


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,以
,以![]() 的中點
的中點![]() 為圓心,以
為圓心,以![]() 的長為直徑的
的長為直徑的![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 的切線
的切線![]() ,交
,交![]() 于點
于點![]() .
.
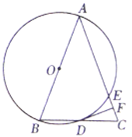
(1)求證:![]() ;
;
(2)填空:
①若![]() ,
,![]() ,則
,則![]() 的面積為____;
的面積為____;
②當![]() 的度數為____時,四邊形
的度數為____時,四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
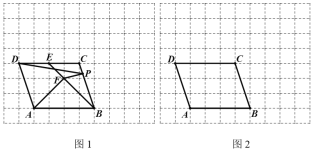
【題目】如圖1,在每個小正方形的邊長為1的網格中,點A、B、C、D均在格點上.點E為直線CD上的動點,連接BE,作AF⊥BE于F.點P為BC邊上的動點,連接DP和PF.
(Ⅰ)當點E為CD邊的中點時,△ABF的面積為 ;
(Ⅱ)當DP+PF最短時,請在圖2所示的網格中,用無刻度的直尺畫出點P,并簡要說明點P的位置是如何找到的(不要求證明) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0對稱軸為直線x=1,與x軸的一個交點坐標為(﹣1,0),其部分圖象如圖所示,下列結論:①abc<0;②4ac<b2;③方程ax2+bx+c=0的兩個根是x1=﹣1,x2=3;④3a+c>0;⑤當y≥0時,x的取值范圍是﹣1≤x≤3.其中結論正確的個數是( )
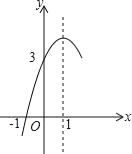
A. 1個B. 2個C. 3D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在平面直角坐標系中,四邊形ABCD是菱形,其中B點坐標是(8,2),D點坐標是(0,2),點A在x軸上,則菱形ABCD的周長是( )
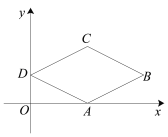
A.2![]()
B.8
C.8![]()
D.12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表中給出![]() ,
,![]() ,
,![]() 三種手機通話的收費方式.
三種手機通話的收費方式.
收費方式 | 月通話費/元 | 包時通話時間/ | 超時費/(元/ |
|
|
|
|
|
|
|
|
|
| 不限時 |
(1)設月通話時間為![]() 小時,則方案
小時,則方案![]() ,
,![]() ,
,![]() 的收費金額
的收費金額![]() ,
,![]() ,
,![]() 都是
都是![]() 的函數,請分別求出這三個函數解析式.
的函數,請分別求出這三個函數解析式.
(2)填空:
若選擇方式![]() 最省錢,則月通話時間
最省錢,則月通話時間![]() 的取值范圍為______;
的取值范圍為______;
若選擇方式![]() 最省錢,則月通話時間
最省錢,則月通話時間![]() 的取值范圍為______;
的取值范圍為______;
若選擇方式![]() 最省錢,則月通話時間
最省錢,則月通話時間![]() 的取值范圍為______;
的取值范圍為______;
(3)小王、小張今年![]() 月份通話費均為
月份通話費均為![]() 元,但小王比小張通話時間長,求小王該月的通話時間.
元,但小王比小張通話時間長,求小王該月的通話時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場要修建一個地下停車場,停車場的入口設計示意圖如圖所示,其中斜坡的傾斜角為18°,一樓到地下停車場地面的距離CD=2.8米,一樓到地平線的距離BC=1米.
(1)為保證斜坡的傾斜角為18°,應在地面上距點B多遠的A處開始斜坡的施工?(結果精確到0.1米)
(2)如果給該商場送貨的貨車高度為2.5米,那么按這樣的設計能否保證貨車順利進入地下停車場?請說明理由.(參考數據:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】松立商店準備從永波機械廠購進甲、乙兩種零件進行銷售,若甲種零件的進價是乙種零件進價的![]() ,用1600元單獨購進一種零件時,購進甲種零件的數量比乙種零件多4件.
,用1600元單獨購進一種零件時,購進甲種零件的數量比乙種零件多4件.
(1)求每個甲種零件,每個乙種零件的進價分別為多少元?
(2)松立商店購進甲、乙兩種零件共102個,準備將零件批發給零售商.甲種零件的批發價是100元,乙種零件的批發價是130元,松立商店計劃從零售商處的獲利超過2284元,通過計算求出松立商店最多給零售商批發多少個甲種零件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com