
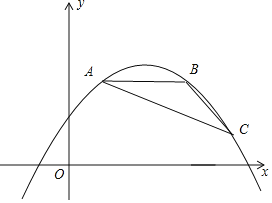
【題目】如圖,點A,B,C都在拋物線y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
<a<0)上,AB∥x軸,∠ABC=135°,且AB=4.
(1)填空:拋物線的頂點坐標為 (用含m的代數式表示);
(2)求△ABC的面積(用含a的代數式表示);
(3)若△ABC的面積為2,當2m﹣5≤x≤2m﹣2時,y的最大值為2,求m的值.
【答案】(1)(m,2m﹣5);(2)S△ABC =﹣![]() ;(3)m的值為
;(3)m的值為![]() 或10+2
或10+2![]() .
.
【解析】(1)利用配方法將二次函數解析式由一般式變形為頂點式,此題得解;
(2)過點C作直線AB的垂線,交線段AB的延長線于點D,由AB∥x軸且AB=4,可得出點B的坐標為(m+2,4a+2m5),設BD=t,則點C的坐標為(m+2+t,4a+2m5t),利用二次函數圖象上點的坐標特征可得出關于t的一元二次方程,解之取其正值即可得出t值,再利用三角形的面積公式即可得出S△ABC的值;
(3)由(2)的結論結合S△ABC=2可求出a值,分三種情況考慮:①當m>2m2,即m<2時,x=2m2時y取最大值,利用二次函數圖象上點的坐標特征可得出關于m的一元二次方程,解之可求出m的值;②當2m5≤m≤2m2,即2≤m≤5時,x=m時y取最大值,利用二次函數圖象上點的坐標特征可得出關于m的一元一次方程,解之可求出m的值;③當m<2m5,即m>5時,x=2m5時y取最大值,利用二次函數圖象上點的坐標特征可得出關于m的一元一次方程,解之可求出m的值.綜上即可得出結論.
(1)∵y=ax2﹣2amx+am2+2m﹣5=a(x﹣m)2+2m﹣5,
∴拋物線的頂點坐標為(m,2m﹣5),
故答案為:(m,2m﹣5);
(2)過點C作直線AB的垂線,交線段AB的延長線于點D,如圖所示,
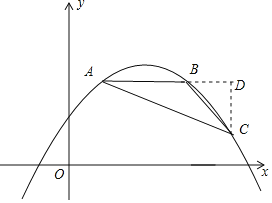
∵AB∥x軸,且AB=4,
∴點B的坐標為(m+2,4a+2m﹣5),
∵∠ABC=135°,
∴設BD=t,則CD=t,
∴點C的坐標為(m+2+t,4a+2m﹣5﹣t),
∵點C在拋物線y=a(x﹣m)2+2m﹣5上,
∴4a+2m﹣5﹣t=a(2+t)2+2m﹣5,
整理,得:at2+(4a+1)t=0,
解得:t1=0(舍去),t2=﹣![]() ,
,
∴S△ABC=![]() ABCD=﹣
ABCD=﹣![]() ;
;
(3)∵△ABC的面積為2,
∴﹣![]() =2,
=2,
解得:a=﹣![]() ,
,
∴拋物線的解析式為y=﹣![]() (x﹣m)2+2m﹣5.
(x﹣m)2+2m﹣5.
分三種情況考慮:
①當m>2m﹣2,即m<2時,有﹣![]() (2m﹣2﹣m)2+2m﹣5=2,
(2m﹣2﹣m)2+2m﹣5=2,
整理,得:m2﹣14m+39=0,
解得:m1=7﹣![]() (舍去),m2=7+
(舍去),m2=7+![]() (舍去);
(舍去);
②當2m﹣5≤m≤2m﹣2,即2≤m≤5時,有2m﹣5=2,解得:m=![]() ;
;
③當m<2m﹣5,即m>5時,有﹣![]() (2m﹣5﹣m)2+2m﹣5=2,
(2m﹣5﹣m)2+2m﹣5=2,
整理,得:m2﹣20m+60=0,
解得:m3=10﹣2![]() (舍去),m4=10+2
(舍去),m4=10+2![]() .
.
綜上所述:m的值為![]() 或10+2
或10+2![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,∠1=∠2.求證:∠3 +∠4=180°.
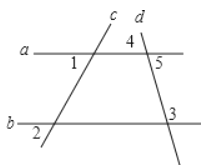
證明:∵∠1=∠2(已知)
∴ a∥b( )
∴∠3 +∠5=180° (兩直線平行,同旁內角互補)
又 ∵∠4=∠5 ( )
∴∠3 +∠4=180° (等量代換)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
材料一:對于一個兩位數![]() ,交換它的個位和十位數字得到的新數
,交換它的個位和十位數字得到的新數![]() 叫這個兩位數
叫這個兩位數![]() 的“倒序數”.如:23的倒序數是32,50的倒序數是05.
的“倒序數”.如:23的倒序數是32,50的倒序數是05.
材料二:對于一個兩位數![]() ,若它的個位數字與十位數字的和小于等于9,則把個位數字與十位數字的和插入到這個兩位數中間得到的新數叫這個兩位數
,若它的個位數字與十位數字的和小于等于9,則把個位數字與十位數字的和插入到這個兩位數中間得到的新數叫這個兩位數![]() 的“凸數”.如23的凸數是253.
的“凸數”.如23的凸數是253.
(1)請求出42的“倒序數”與“凸數”;38有“凸數”嗎?為什么?
(2)若一個兩位數與它的“倒序數”的和的4倍比這個兩位數的“凸數”小132,請求出這個兩位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
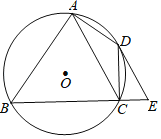
【題目】如圖,四邊形ABCD內接于⊙O,∠BAD=90°,點E在BC的延長線上,且∠DEC=∠BAC.
(1)求證:DE是⊙O的切線;
(2)若AC∥DE,當AB=8,CE=2時,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AB邊的中點,沿EC對折矩形ABCD,使B點落在點P處,折痕為EC,連結AP并延長AP交CD于F點,連結CP并延長CP交AD于Q點.給出以下結論:
①四邊形AECF為平行四邊形;
②∠PBA=∠APQ;
③△FPC為等腰三角形;
④△APB≌△EPC.
其中正確結論的個數為( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市的空氣質量情況,從環境監測網隨機抽取了若干天的空氣質量情況作為樣本進行統計,繪制了如圖所示的條形統計圖和扇形統計圖(部分信息未給出).請你根據圖中提供的信息,解答下列問題:
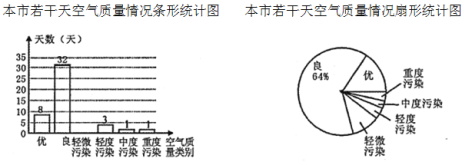
(1)通過計算補全條形統計圖;
(2)求扇形統計圖中表示“輕度污染”的扇形的圓心角度數;
(3)請估計我市這一年(365天)達到“優”和“良”的總天數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數軸上5與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]() ;
;
在數軸上![]() 與3所對的兩點之間的距離:
與3所對的兩點之間的距離:![]() ;
;
在數軸上![]() 與
與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]() ;
;
在數軸上點![]() 、
、![]() 分別表示數
分別表示數![]() 、
、![]() ,則
,則![]() 、
、![]() 兩點之間的距離
兩點之間的距離![]()
![]()
回答下列問題:
(1)數軸上表示![]() 和
和![]() 的兩點之間的距離是_________;
的兩點之間的距離是_________;
數軸上表示數![]() 和3的兩點之間的距離表示為_________;
和3的兩點之間的距離表示為_________;
數軸上表示數_______和________的兩點之間的距離表為![]() ;
;
(2)七年級研究性學習小組在數學老師指導下,對式子![]() 進行探究:
進行探究:
①請你借助于數軸進行探究:當表示數![]() 的點在
的點在![]() 與3之間移動時,
與3之間移動時,![]() 的值總是一個固定的值為:____________.
的值總是一個固定的值為:____________.
②請你借助于數軸進行探究:如果要使![]() ,那么數軸上表示點的數
,那么數軸上表示點的數![]() __________.
__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,三角形紙片ABC中,∠A=65°,∠B=75°,將∠C沿DE對折,使點C落在ΔABC外的點![]() 處,若∠1=20°,則∠2的度數為( )
處,若∠1=20°,則∠2的度數為( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com