
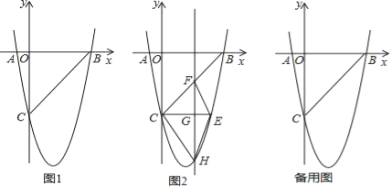
【題目】如圖1,在平面直角坐標系中,已知拋物線y=ax2+bx-5與x軸交于A(-1,0),B(5,0)兩點,與y軸交于點C.
(1)求拋物線的函數表達式;
(2)如圖2,CE∥x軸與拋物線相交于點E,點H是直線CE下方拋物線上的動點,過點H且與y軸平行的直線與BC,CE分別交于點F,G,試探究當點H運動到何處時,四邊形CHEF的面積最大,求點H的坐標及最大面積;
(3)若點K為拋物線的頂點,點M(4,m)是該拋物線上的一點,在x軸,y軸上是否存在點P,Q,使四邊形PQKM的周長最小,若沒有,說明理由;若有,求出點P,Q的坐標.
【答案】(1)y=x2-4x-5;(2)H(![]() ,
,![]() ),面積最大為
),面積最大為![]() ;(3)存在,P(
;(3)存在,P(![]() ,0),Q(0,-
,0),Q(0,-![]() ).
).
【解析】
(1)根據待定系數法直接求出拋物線解析式即可;
(2)設H(t,t2﹣4t﹣5),求出直線BC的解析式,即可表示出點F的坐標,進而求出四邊形CHEF的面積與t的函數關系式,利用二次函數求最值即可;
(3)利用對稱性找出點P,Q的位置,進而求出P,Q的坐標.
解:(1)∵點A(﹣1,0),B(5,0)在拋物線y=ax2+bx﹣5上,
∴![]() ,
,
解得![]() ,
,
∴拋物線的表達式為y=x2﹣4x﹣5,
(2)設H(t,t2﹣4t﹣5),
∵CE∥x軸,
∴點E的縱坐標為﹣5,
∵E在拋物線上,
∴x2﹣4x﹣5=﹣5,
∴x=0(舍)或x=4,
∴E(4,﹣5),
∴CE=4,
設直線BC的解析式為y=kx+c
將B(5,0),C(0,﹣5)代入,得
![]()
解得:![]()
∴直線BC的解析式為y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣![]() )2+
)2+![]() ,
,
∵CE∥x軸,HF∥y軸,
∴CE⊥HF,
∴S四邊形CHEF=![]() CEHF=﹣2(t﹣
CEHF=﹣2(t﹣![]() )2+
)2+![]() ,
,
∵-2<0
∴當t=![]() 時,S四邊形CHEF最大,最大值為
時,S四邊形CHEF最大,最大值為![]()
∴H(![]() ,﹣
,﹣![]() );
);
(3)如圖2,四邊形PQKM的周長=PM+PQ+QK+KM(其中KM為定值)
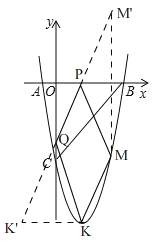
∵K為拋物線的頂點,y=x2-4x-5=(x-2)2-9
∴K(2,﹣9),
∴K關于y軸的對稱點K′(﹣2,﹣9),
∵M(4,m)在拋物線上,
∴m=16-16-5=-5
∴M(4,﹣5),
∴點M關于x軸的對稱點M′(4,5),
連接K′M′,分別交x軸于點P,交y軸于點Q
∴此時PM=PM′,QK=QK′
∴此時四邊形PQKM的周長=PM+PQ+QK+KM= PM′+PQ +QK′+KM=M′K′+KM,根據兩點之間線段最短,此時四邊形PQKM的周長最小
設直線K′M′的解析式為y=ex+d
將K′、M′的坐標代入,得
![]()
解得: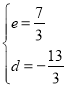
∴直線K′M′的解析式為y=![]() ,
,
當y=0時,解得x=![]() ;當x=0時,解得y=
;當x=0時,解得y=![]()
∴P(![]() ,0),Q(0,﹣
,0),Q(0,﹣![]() ).
).


科目:初中數學 來源: 題型:
【題目】某校在開展讀書交流活動中全體師生積極捐書.為了解所捐書籍的種類,對部分書籍進行了抽樣調查,李老師根據調查數據繪制了如圖所示不完整統計圖.請根據統計圖回答下面問題: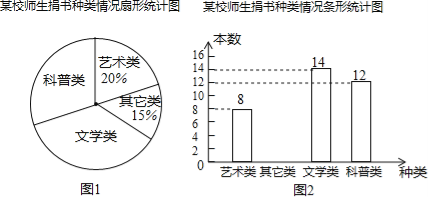
(1)本次抽樣調查的書籍有多少本?請補全條形統計圖;
(2)求出圖1中表示文學類書籍的扇形圓心角度數;
(3)本次活動師生共捐書1200本,請估計有多少本科普類書籍?
查看答案和解析>>
科目:初中數學 來源: 題型:
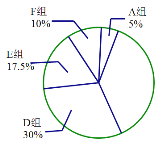
【題目】某社區招募了40位居民參加“眾志成城,抗擊疫情”志愿者服務活動,對志愿者一天的服務時長進行調查,由調查結果繪制了如下不完整的頻數分布表和扇形統計圖.
頻數分布表
組別 | 時間/小時 | 頻數/人數 |
A組 | 0≤ | 2 |
B組 | 1≤ | m |
C組 | 2≤ | 10 |
D組 | 3≤ | 12 |
E組 | 4≤ | 7 |
F組 |
| 4 |
扇形統計圖
請根據圖表中的信息解答下列問題:
(1)求頻數分布表中的![]() 的值;
的值;
(2)求B組,C組在扇形統計圖中分別對應扇形的圓心角的度數,并補全扇形統計圖;
(3)已知F組的志愿者中,只有1名女志愿者.要從該組中選取兩名志愿者分發生活物資,請用樹狀圖或列表的方法求2名志愿恰好都是男士的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c經過點A(﹣2,5),與x軸相交于B(﹣1,0),C(3,0)兩點.
(1)求拋物線的函數表達式;
(2)點D在拋物線的對稱軸上,且位于x軸的上方,將△BCD沿直線BD翻折得到△BC′D,若點C′恰好落在拋物線的對稱軸上,求點C′和點D的坐標;

查看答案和解析>>
科目:初中數學 來源: 題型:
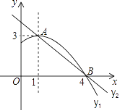
【題目】如圖是拋物線y1=ax2+bx+c(a≠0)圖象的一部分,拋物線的頂點坐標A(1,3),與x軸的一個交點B(4,0),直線y2=mx+n(m≠0)與拋物線交于A,B兩點,下列結論: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有兩個相等的實數根;④拋物線與x軸的另一個交點是(﹣1,0);⑤當1<x<4時,有y2<y1 ,
其中正確的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 、
、![]() 是兩座現代化城市,
是兩座現代化城市,![]() 是一個古城遺址,
是一個古城遺址,![]() 城在
城在![]() 城的北偏東
城的北偏東![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正東方向,且
城的正東方向,且![]() 城與
城與![]() 城相距120千米,現在
城相距120千米,現在![]() 、
、![]() 兩城市修建一條筆直的高速公路.
兩城市修建一條筆直的高速公路.
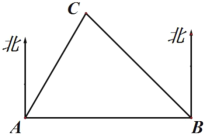
(1)請你計算公路![]() 的長度(結果保留根號);
的長度(結果保留根號);
(2)若以![]() 為圓心,以60千米為半徑的圓形區域內為古跡和地下文物保護區,請你分析公路
為圓心,以60千米為半徑的圓形區域內為古跡和地下文物保護區,請你分析公路![]() 會不會穿越這個保護區,并說明理由.
會不會穿越這個保護區,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
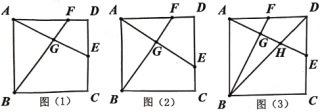
【題目】如圖,正方形ABCD的邊長為6,E、F分別是邊CD、AD上動點,AE和BF交于點G.
(1)如圖(1),若E為邊CD的中點,AF=2FD,求AG的長.
(2)如圖(2),若點F在AD上從A向D運動,點E在DC上從D向C運動,兩點同時出發,同時到達各自終點,求在運動過程中,點G運動的路徑長.
(3)如圖(3),若E、F分別是邊CD、AD上的中點,BD與AE交于點H,求∠FBD的正切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市銷售A,B兩款保溫杯,已知B款保溫杯的銷售單價比A款保溫杯多10元,用480元購買B款保溫杯的數量與用360元購買A款保溫杯的數量相同.
(1)A,B兩款保溫杯的銷售單價各是多少元?
(2)由于需求量大,A,B兩款保溫杯很快售完,該超市計劃再次購進這兩款保溫杯共120個,且A款保溫杯的數量不少于B保溫杯的2倍,A保溫杯的售價不變,B款保溫杯的銷售單價降低10%,兩款保溫杯的進價每個均為20元,應如何進貨才能使這批保溫杯的銷售利潤最大,最大利潤是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com