
【題目】如圖,在![]() 中,
中,![]() ,以斜邊
,以斜邊![]() 上的中線
上的中線![]() 為直徑作
為直徑作![]() ,分別與
,分別與![]() 、
、![]() 交于點
交于點![]() 、
、![]() .
.
(1)過點![]() 作
作![]() 的切線
的切線![]() 與
與![]() 相交于點
相交于點![]() ,求證:
,求證:![]() ;
;
(2)連接![]() ,求證:
,求證:![]() .
.
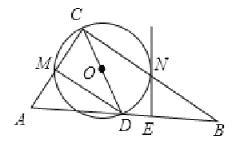
【答案】(1)見解析;(2)見解析;
【解析】
(1)連接ON,如圖,根據斜邊上的中線等于斜邊的一半得到CD=AD=DB,則∠1=∠B,再證明∠2=∠B得到ON∥DB,接著根據切線的性質得到ON⊥NE,然后利用平行線的性質得到結論;
(2)連接DN,如圖,根據圓周角定理得到∠CMD=∠CND=90°,則可判斷四邊形CMDN為矩形,所以DM=CN,然后證明CN=BN,從而得到MD=NB.
證明:(1)連接ON,如圖,
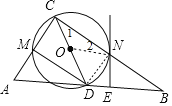
∵CD為斜邊AB上的中線,
∴CD=AD=DB,
∴∠1=∠B,
∵OC=ON,
∴∠1=∠2,
∴∠2=∠B,
∴ON∥DB,
∵NE為切線,
∴ON⊥NE,
∴NE⊥AB;
(2)連接DN,如圖,

∵CD為直徑,
∴∠CMD=∠CND=90°,
而∠MCB=90°,
∴四邊形CMDN為矩形,
∴DM=CN,
∵DN⊥BC,∠1=∠B,
∴CN=BN,
∴MD=NB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+3與x軸交于A、B兩點,過點A的直線l與拋物線交于點C,其中A點的坐標是(1,0),C點坐標是(4,3).
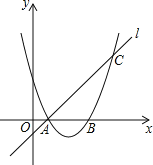
(1)求拋物線的解析式;
(2)設直線l與y軸交于點D,拋物線交y軸于點E,則△DBE的面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知二次函數y=ax2+bx+c的y與x的部分對應值如下表;
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列結論:①拋物線的開口向下;②其圖象的對稱軸為x=1;③當x﹤l時,函數值y隨x 的增大而增大;④方程ax2+bx+c=0有一個根大于4.其中正確的結論有( )
A. 4個B. 1個C. 3個D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,動點
,動點 ![]() 從點
從點 ![]() 出發以
出發以 ![]() 的速度沿
的速度沿 ![]() 的方向運動,動點
的方向運動,動點 ![]() 從點
從點 ![]() 出發以
出發以 ![]() 的速度沿
的速度沿 ![]() 方向運動,
方向運動,![]() ,
,![]() 兩點同時出發,當
兩點同時出發,當 ![]() 到達點
到達點 ![]() 時停止運動,點
時停止運動,點 ![]() 也隨之停止,設運動的時間為
也隨之停止,設運動的時間為 ![]() .
.
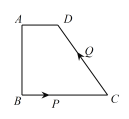
(1)求線段 ![]() 的長;
的長;
(2)![]() 為何值時,線段
為何值時,線段 ![]() 將四邊形
將四邊形 ![]() 的面積分為
的面積分為 ![]() 兩部分.
兩部分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】泗縣某童裝專賣店在銷售中發現,一款童裝每件進價為![]() 元,利潤為
元,利潤為![]() 元時,每天可售出
元時,每天可售出![]() 件,為了迎接“六一”兒童節,商店決定采取適當的降價措施,以擴大銷售量增加利潤,經市場調查發現,如果每件童裝降價
件,為了迎接“六一”兒童節,商店決定采取適當的降價措施,以擴大銷售量增加利潤,經市場調查發現,如果每件童裝降價![]() 元,那么平均每天可售出
元,那么平均每天可售出![]() 件.
件.
(1)設每件童裝降價![]() 元,每天可售出 件,每件盈利 元,若商家平均每天能贏利
元,每天可售出 件,每件盈利 元,若商家平均每天能贏利![]() 元,每件童裝應降價多少元?根據題意,列出方程 .
元,每件童裝應降價多少元?根據題意,列出方程 .
(2)利用配方法解答(1)中所列方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小林準備進行如下操作試驗:把一根長為![]() 的鐵絲剪成兩段,并把每一段各圍成一個正方形.
的鐵絲剪成兩段,并把每一段各圍成一個正方形.
(1)要使這兩個正方形的面積之和等于![]() ,小林該怎么剪?
,小林該怎么剪?
(2)小峰對小林說:“這兩個正方形的面積之和不可能等于![]() .”他的說法對嗎?請說明理由.
.”他的說法對嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】邊長為8的正方形ABCD中,點P在BC邊上,CP=2,點Q為線段AP上一動點,射線BQ與正方形ABCD的一邊交于點R,且AP=BR,那么![]() ____________
____________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九月份,開州本地彌猴桃全面上市,其中新品種金梅彌猴桃因其個大多汁而深受大家喜愛,但彌猴桃一直因保鮮技術問題銷售量不多,今年終于突破保鮮技術,水果售量明顯上升.永輝超市準備大量進貨,已知去年同期普通彌猴桃進價3元/斤,金梅彌猴桃進價10元/斤,去年九月共進貨900斤.
(1)若去年九月兩種彌猴桃進貨總價不超過6200元,則金梅彌猴桃最多能購進多少斤?
(2)若永輝超市今年九月上半月共購進1000斤彌猴桃,其中普通彌猴桃進價與去年相同,金梅彌猴桃進價降4元,結果普通彌猴桃按8元/斤,金梅彌猴桃按16元/斤的價格賣出后共獲利8000元,下半月因臨近祖國七十華誕,水果需量上升,兩種彌猴桃進價在上半月基礎上保持不變,售價一路上漲,超市調整計劃,普通彌猴桃進貨量與上半月持平,售價下降a%吸引顧客;金梅彌猴桃進貨量上漲生![]() %,售價上漲2a%,最后截至九月底,下半月獲利比上半月的2倍少400元,求a的值.
%,售價上漲2a%,最后截至九月底,下半月獲利比上半月的2倍少400元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
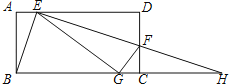
【題目】如圖,將矩形ABCD的一個角翻折,使得點D恰好落在BC邊上的點G處,折痕為EF,若EB為∠AEG的平分線,EF和BC的延長線交于點H.下列結論中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面積相等;⑤若![]() ,則
,則![]() .以上命題,正確的有( )
.以上命題,正確的有( )
A.2個B.3個C.4個D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com