
【題目】如圖,點(diǎn)A、B和線段CD都在數(shù)軸上,點(diǎn)A,C,D,B起始位置所表示的數(shù)分別為-2,0,3,12;線段CD沿?cái)?shù)軸的正方向以每秒1個(gè)單位長度的速度運(yùn)動(dòng),運(yùn)動(dòng)時(shí)間為1秒.
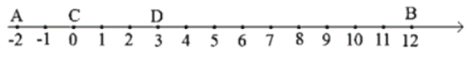
(1)當(dāng)![]() =0秒時(shí),AC的長為________,當(dāng)
=0秒時(shí),AC的長為________,當(dāng)![]() =2秒時(shí),AC的長為________;
=2秒時(shí),AC的長為________;
(2)用含有![]() 的代數(shù)式表示AC的線段長為________;
的代數(shù)式表示AC的線段長為________;
(3)當(dāng)![]() =__________秒時(shí),AC-BD=5;當(dāng)
=__________秒時(shí),AC-BD=5;當(dāng)![]() =___________秒時(shí)AC+BD=15;
=___________秒時(shí)AC+BD=15;
(4)若點(diǎn)A與線段CD同時(shí)出發(fā)沿?cái)?shù)軸的正方向移動(dòng),點(diǎn)A的速度為每秒2個(gè)單位長度,在移動(dòng)過程中,是否存在某一時(shí)刻使得AC=2BD,若存在,請直接求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)2,4;(2)![]() +2;(3)6,11;(4)16秒和
+2;(3)6,11;(4)16秒和![]() 秒
秒
【解析】
(1)依據(jù)A、C兩點(diǎn)間的距離=|![]() -
-![]() |求解即可;
|求解即可;
(2)![]() 秒后點(diǎn)C運(yùn)動(dòng)的距離為
秒后點(diǎn)C運(yùn)動(dòng)的距離為![]() 個(gè)單位長度,從而點(diǎn)C表示的數(shù);根據(jù)A、C兩點(diǎn)間的距離=|
個(gè)單位長度,從而點(diǎn)C表示的數(shù);根據(jù)A、C兩點(diǎn)間的距離=|![]() -
-![]() |求解即可.
|求解即可.
(3)1秒后點(diǎn)C運(yùn)動(dòng)的距離為![]() 個(gè)單位長度,點(diǎn)D運(yùn)動(dòng)的距離為
個(gè)單位長度,點(diǎn)D運(yùn)動(dòng)的距離為![]() 個(gè)單位長度,從而可得到點(diǎn)A、點(diǎn)D表示的數(shù);根據(jù)兩點(diǎn)間的距離=|
個(gè)單位長度,從而可得到點(diǎn)A、點(diǎn)D表示的數(shù);根據(jù)兩點(diǎn)間的距離=|![]() -
-![]() |表示出AC、BD.根據(jù)AC-BD=5和AC+BD=15得到關(guān)于
|表示出AC、BD.根據(jù)AC-BD=5和AC+BD=15得到關(guān)于![]() 的含絕對值符號的一元次方程,分別解方程即可得出結(jié)論;
的含絕對值符號的一元次方程,分別解方程即可得出結(jié)論;
(4)假設(shè)能夠相等,找出AC、BD,根據(jù)AC=2BD即可列出關(guān)于![]() 的含絕對值符號的一元一次方程,解方程即可得出結(jié)論.
的含絕對值符號的一元一次方程,解方程即可得出結(jié)論.
解:(1)當(dāng)![]() =0秒時(shí),AC=|-2-0|=|-2|=2;
=0秒時(shí),AC=|-2-0|=|-2|=2;
當(dāng)![]() =2秒時(shí),移動(dòng)后C表示的數(shù)為2,
=2秒時(shí),移動(dòng)后C表示的數(shù)為2,
∴AC=|-2-2|=4.
故答案為:2;4.
(2)點(diǎn)A表示的數(shù)為-2,點(diǎn)C表示的數(shù)為![]() ;
;
.AC=|-2-![]() |=
|=![]() +2.
+2.
故答案為![]() +2.
+2.
(3)∵![]() 秒后點(diǎn)C運(yùn)動(dòng)的距離為
秒后點(diǎn)C運(yùn)動(dòng)的距離為![]() 個(gè)單位長度,點(diǎn)D運(yùn)動(dòng)的距離為
個(gè)單位長度,點(diǎn)D運(yùn)動(dòng)的距離為![]() 個(gè)單位長度.
個(gè)單位長度.
∴C表示的數(shù)是![]() ,D表示的數(shù)是3+
,D表示的數(shù)是3+![]() ,
,
∴AC=![]() +2,BD=|12-(3+
+2,BD=|12-(3+![]() )|,
)|,
∵AC-BD=5,
∴![]() +2-|12-(
+2-|12-(![]() +3)|=5,
+3)|=5,
即![]() +2-|9-
+2-|9-![]() |=5,
|=5,
當(dāng)![]() 時(shí),t+2-(9-t)=5,
時(shí),t+2-(9-t)=5,
解得:![]() =6;
=6;
當(dāng)t>9時(shí),t+2+(9-t)=5,此時(shí)無解;
∴t=6.
∴當(dāng)![]() =6秒時(shí)AC-BD=5;
=6秒時(shí)AC-BD=5;
∵AC+BD=15,
∴![]() +2+|12-(
+2+|12-(![]() +3) |=15,
+3) |=15,
即![]() +2+|9-
+2+|9-![]() |=15
|=15
當(dāng)![]() 時(shí),t+2+(9-t)=15,此時(shí)無解;
時(shí),t+2+(9-t)=15,此時(shí)無解;
當(dāng)t>9時(shí),t+2-(9-t)=15,解得t=11;
當(dāng)![]() =11秒時(shí)AC+BD=15,
=11秒時(shí)AC+BD=15,
故答案為6,11;
(4)假設(shè)能相等,則點(diǎn)A表示的數(shù)為2![]() -2,C表示的數(shù)為
-2,C表示的數(shù)為![]() ,D表示的數(shù)為
,D表示的數(shù)為![]() +3,B表示的數(shù)為12,
+3,B表示的數(shù)為12,
∴AC=|2![]() -2-
-2-![]() |=|
|=|![]() -2|,BD=|
-2|,BD=|![]() +3-12|=|
+3-12|=|![]() -9|,
-9|,
∵AC=2BD,
∴|![]() -2|=2|
-2|=2|![]() -9|,
-9|,
∴|![]() -2|=|2
-2|=|2![]() -18|
-18|
解得:![]() =16,
=16,![]() .
.
故在運(yùn)動(dòng)的過程中使得AC=2BD,此時(shí)運(yùn)動(dòng)的時(shí)間為16秒和![]() 秒.
秒.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達(dá)標(biāo)測試卷系列答案
芒果教輔達(dá)標(biāo)測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A. “明天降雨的概率是60%”表示明天有60%的時(shí)間都在降雨
B. “拋一枚硬幣正面朝上的概率為![]() ”表示每拋2次就有一次正面朝上
”表示每拋2次就有一次正面朝上
C. “彩票中獎(jiǎng)的概率為1%”表示買100張彩票肯定會(huì)中獎(jiǎng)
D. “拋一枚正方體骰子,朝上的點(diǎn)數(shù)為2的概率為![]() ”表示隨著拋擲次數(shù)的增加,“拋出朝上的點(diǎn)數(shù)為2”這一事件發(fā)生的概率穩(wěn)定在
”表示隨著拋擲次數(shù)的增加,“拋出朝上的點(diǎn)數(shù)為2”這一事件發(fā)生的概率穩(wěn)定在![]() 附近
附近
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若關(guān)于x的一元二次方程x2﹣2(2﹣k)x+k2+12=0有實(shí)數(shù)根α、β.
(1)求實(shí)數(shù)k的取值范圍;
(2)設(shè)![]() ,求t的最小值.
,求t的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度數(shù);
(2)若∠DOE=n°,求∠AOB的度數(shù);
(3)若∠DOE+∠AOB=180°,求∠AOB與∠DOE的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有一些相同的房間需要粉刷墻面.一天3名一級技工去粉刷8個(gè)房間,結(jié)果其中有40m2墻面未來得及粉刷;同樣時(shí)間內(nèi)5名二級技工剛好粉刷了10個(gè)房間,每名一級技工比二級技工一天多粉刷20m2墻面.
(1)一級技工和二級技工每人每天各粉刷多少墻面?
(2)現(xiàn)有若干間這樣的房間需要在規(guī)定的時(shí)間內(nèi)粉刷完墻面,若安排一名一級技工單獨(dú)粉刷,可比規(guī)定時(shí)間提前1天完成;若安排一名二級技工單獨(dú)完成,到規(guī)定時(shí)間還有4間房間沒粉刷.需要粉刷的房間一共有多少間?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在數(shù)軸上有三個(gè)點(diǎn)A,B,C,回答下列問題:
(1)若將點(diǎn)B向右移動(dòng)6個(gè)單位后,三個(gè)點(diǎn)所表示的數(shù)中最小的數(shù)是多少?
(2)在數(shù)軸上找一點(diǎn)D,使點(diǎn)D到A,C兩點(diǎn)的距離相等,寫出點(diǎn)D表示的數(shù);
(3)在點(diǎn)B左側(cè)找一點(diǎn)E,使點(diǎn)E到點(diǎn)A的距離是到點(diǎn)B的距離的2倍,并寫出點(diǎn)E表示的數(shù).
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在圖中網(wǎng)格上按要求畫出圖形,并回答問題:
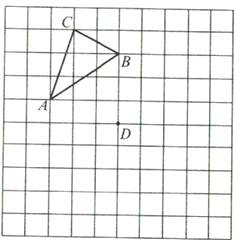
(1)如果將三角形![]() 平移,使得點(diǎn)
平移,使得點(diǎn)![]() 平移到圖中點(diǎn)
平移到圖中點(diǎn)![]() 位置,點(diǎn)
位置,點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 的對應(yīng)點(diǎn)分別為點(diǎn)
的對應(yīng)點(diǎn)分別為點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() ,請畫出三角形
,請畫出三角形![]() ;
;
(2)畫出三角形![]() 關(guān)于點(diǎn)
關(guān)于點(diǎn)![]() 成中心對稱的三角形
成中心對稱的三角形![]() .
.
(3)三角形![]() 與三角形
與三角形![]() ______(填“是”或“否”)關(guān)于某個(gè)點(diǎn)成中心對稱?如果是,請?jiān)趫D中畫出這個(gè)對稱中心,并記作點(diǎn)
______(填“是”或“否”)關(guān)于某個(gè)點(diǎn)成中心對稱?如果是,請?jiān)趫D中畫出這個(gè)對稱中心,并記作點(diǎn)![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校的春季趣味運(yùn)動(dòng)會(huì)深受學(xué)生喜愛,該校體育教師為了了解該次運(yùn)動(dòng)會(huì)中四個(gè)項(xiàng)目的受歡迎程度,隨機(jī)抽取了部分學(xué)生進(jìn)行問卷調(diào)查,被調(diào)查學(xué)生須從“托球跑、擲飛盤、推小車、鴨子步”四個(gè)項(xiàng)目中選擇自己最喜歡的一項(xiàng).
根據(jù)調(diào)查結(jié)果,體育教師繪制了圖1和圖2兩個(gè)統(tǒng)計(jì)圖(均未完成),請根據(jù)圖1和圖2的信息,解答下列問題.
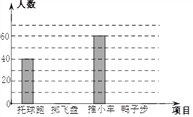
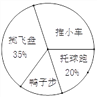
(1)此次共調(diào)查了多少名學(xué)生?
(2)將條形統(tǒng)計(jì)圖補(bǔ)充完整.
(3)圖2中“鴨子步”所在扇形圓心角為多少度?
(4)若全校有學(xué)生1600人,估計(jì)該校喜歡“推小車”項(xiàng)目的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校有3000名學(xué)生.為了解全校學(xué)生的上學(xué)方式,該校數(shù)學(xué)興趣小組以問卷調(diào)查的形式,隨機(jī)調(diào)查了該校部分學(xué)生的主要上學(xué)方式(參與問卷調(diào)查的學(xué)生只能從以下六個(gè)種類中選擇一類),并將調(diào)查結(jié)果繪制成如下不完整的統(tǒng)計(jì)圖.
種類 | A | B | C | D | E | F |
上學(xué)方式 | 電動(dòng)車 | 私家車 | 公共交通 | 自行車 | 步行 | 其他 |
某校部分學(xué)生主要上學(xué)方式扇形統(tǒng)計(jì)圖某校部分學(xué)生主要上學(xué)方式條形統(tǒng)計(jì)圖
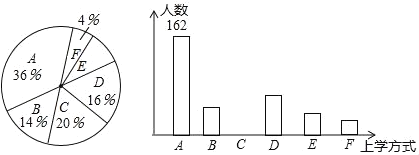
根據(jù)以上信息,回答下列問題:
(1)參與本次問卷調(diào)查的學(xué)生共有____人,其中選擇B類的人數(shù)有____人.
(2)在扇形統(tǒng)計(jì)圖中,求E類對應(yīng)的扇形圓心角α的度數(shù),并補(bǔ)全條形統(tǒng)計(jì)圖.
(3)若將A、C、D、E這四類上學(xué)方式視為“綠色出行”,請估計(jì)該校每天“綠色出行”的學(xué)生人數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com