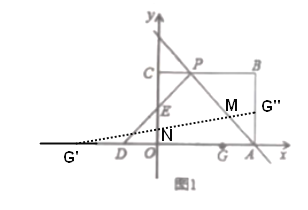
【題目】如圖1，矩形
擺放在平面直角坐標系中，點
在
軸上，點
在
軸上，
，
，過點的直線交矩形的邊
于點
，且點不與點
、重合，過點作
，
交軸于點
，交軸于點
．
（1）若
為等腰直角三角形．
①求直線
的函數(shù)解析式；
②在軸上另有一點
的坐標為
，請在直線和軸上分別找一點
、
，使
的周長最小，并求出此時點的坐標和周長的最小值．
（2）如圖2，過點作
交軸于點
，若以、、、為頂點的四邊形是平行四邊形，求直線
的解析式．
【答案】（1）①直線
解析式
， ②N(0,
),
周長的最小值為
；（2）
.
【解析】
（1）①利用矩形的性質確定A、B、C點的坐標，再利用等腰三角的性質確定
，所以
，確定P點的坐標，再根據A點的坐標確定確定直線AP的函數(shù)表達式. ②作G點關于y軸對稱點G'(-2,0)，作點G關于直線AP對稱點G'(3,1)
連接G'G'交y軸于N，交直線AP于M，此時ΔGMN周長的最小．（2）過P作PM⊥AD于M，先根據等腰三角形三線合一的性質證明DM=MA ，再根據角角邊定理證明ΔODE≌ΔMDP，根據全等三角形的性質求出點P、D的坐標，代入直線解析式得k=2,b=-2，所以直線PE的解析式為y=2x-2.
（1）①∵矩形
，
∴
，
∵
為等腰直角三角形
∴
∵
∴
∵
∴
∴
∴
設直線
解析式
，過點
，點
∴
∴
∴直線解析式
②作
點關于
軸對稱點
，作點關于直線對稱點
連接
交軸于
，交直線于
，此時
周長的最小．
∵
∴直線解析式
當
時，
，∴
∵
∴周長的最小值為
（2）如圖：作
于
∵
∴
且
∴
，且 ∴
∵四邊形
是平行四邊形 ∴
又∵
∴
∴
∴
∵
∴
∴
設直線
的解析式
∴
∴直線解析式
一諾書業(yè)暑假作業(yè)快樂假期云南美術出版社系列答案科目：初中數(shù)學 來源： 題型：
【題目】如圖，給正五邊形的頂點依次編號為
．若從某一頂點開始，沿正五邊形的邊順時針行走，頂點編號的數(shù)字是幾，就走幾個邊長，則稱這種走法為一次“移位”．
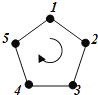
如:小宇同學從編號為
的頂點開始，他應走個邊長，即從
為第一次“移位”，這時他到達編號為
的頂點；然后從
為第二次“移位”，．．．．若小宇同學從編號為
的頂點開始，則第九十九次“移位”后他所處頂點的編號是（ ）
A.B.C.D.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】長方體敞口玻璃罐，長、寬、高分別為16 cm、6 cm和6 cm，在罐內點E處有一小塊餅干碎末，此時一只螞蟻正好在罐外壁，在長方形ABCD中心的正上方2 cm處，則螞蟻到達餅干的最短距離是多少cm.( )
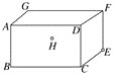
A. 7
B. 
C. 24D. 
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】某校八年級全體同學參加了某項捐款活動，隨機抽查了部分同學捐款的情況統(tǒng)計如圖所示
(1)本次共抽查學生____人，并將條形圖補充完整；
(2)捐款金額的眾數(shù)是_____，平均數(shù)是_____；
(3)在八年級700名學生中，捐款20元及以上(含20元)的學生估計有多少人？
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
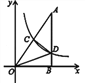
【題目】如圖，Rt△AOB的一條直角邊OB在x軸上，雙曲線
（x＞0）經過斜邊OA的中點C，與另一直角邊交于點D．若
=3，則
的值為_______．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，數(shù)軸上A，B兩點對應的有理數(shù)分別為10和15，點P從點A出發(fā)，以每秒1個單位長度的速度沿數(shù)軸正方向運動，點Q同時從原點O出發(fā)，以每秒2個單位長度的速度沿數(shù)軸正方向運動，設運動時間為t秒．
(1)當0＜t＜5時，用含t的式子填空：
BP＝_______，AQ＝_______；
(2)當t＝2時，求PQ的值；
(3)當PQ＝
AB時，求t的值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】把2018個正整數(shù)1，2，3，4，…，2018按如圖方式排列成一個表.
（1）用如圖方式框住表中任意4個數(shù)，記左上角的一個數(shù)為
，則另三個數(shù)用含的式子表示出來，從小到大依次是__________、___________、_______________（請直接填寫答案）；
（2）用（1）中方式被框住的4個數(shù)之和可能等于2019嗎？如果可能，請求出的值；如果不可能，請說明理由.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】某市水果批發(fā)部門欲將A市的一批水果運往本市銷售，有火車和汽車兩種運輸方式，運輸過程中的損耗均為200元／時。其它主要參考數(shù)據如下：
運輸工具 | 途中平均速度（千米／時） | 運費（元／千米） | 裝卸費用（元） |
火車 | 100 | 15 | 2000 |
汽車 | 80 | 20 | 900 |
(1)如果汽車的總支出費用比火車費用多1100元，你知道本市與A市之間的路程是多少千米嗎？請你列方程解答．
(2)如果A市與某市之間的距離為S千米，且知道火車與汽車在路上耽誤的時間分別為2小時和3.1小時，你若是某市水果批發(fā)部門的經理，要將這種水果從A市運往本市銷售。你將選擇哪種運輸方式比較合算呢？
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com