
���}Ŀ���ⷽ�̣�
��1��x2��4x��3=0��
��2����2x+1��2=��2��x��2��
���𰸡�(1) x1=2+![]() ��x2=2��
��x2=2��![]() ��(2) x1=��3��x2=
��(2) x1=��3��x2=![]()
����������1�����ù�ʽ����һԪ���η��̼��ɣ�
��2�������(xi��ng)��Ȼ������ƽ���ʽ��(du��)��ʽ����߅�M(j��n)����ʽ�ֽ⣬����⼴�ɣ�
�䷽����һԪ���η��̣����}�r(sh��)Ҫע����}���E�Ĝ�(zh��n)�_��(y��ng)�ã�����߅�����ȫƽ��ʽ����߅���鳣��(sh��)��
��1��x2��4x��3=0��
��a=1��b=��4��c=��3��
���=b2��4ac=����4��2��4��1������3��=28��
��x=![]() =2��
=2��![]() ��
��
�tx1=2+![]() ��x2=2��
��x2=2��![]() ��
��
��2����2x+1��2=��2��x��2��
��2x+1+2��x����2x+1��2+x��=0��
��x+3����3x��1��=0��
�tx1=��3��x2=![]() ��
��


 ͬ���p�ɾ���(x��)ϵ�д�
ͬ���p�ɾ���(x��)ϵ�д� �n�nͨ�n�̘�(bi��o)��(zh��n)˼�S�����c����Ӗ(x��n)��ϵ�д�
�n�nͨ�n�̘�(bi��o)��(zh��n)˼�S�����c����Ӗ(x��n)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˽�ijУ�W(xu��)����(du��)A���(qi��ng)���X����B�����x�ߡ���C���Ї�(gu��)Ԋ(sh��)�~���(hu��)����D�������Ї�(gu��)�ˡ��Ă�(g��)�ҕ��(ji��)Ŀ��ϲ��(��i)��r���S�C(j��)��ȡ��һЩ�W(xu��)���M(j��n)���{(di��o)��y(t��ng)Ӌ(j��)��Ҫ��ÿ��ͬ�W(xu��)�x������ֻ���x��һ��(g��)�Լ�ϲ�g�Ĺ�(ji��)Ŀ���������{(di��o)��Y(ji��)���L�Ƴ����ɷ��������Ľy(t��ng)Ӌ(j��)�D����D1�͈D2����
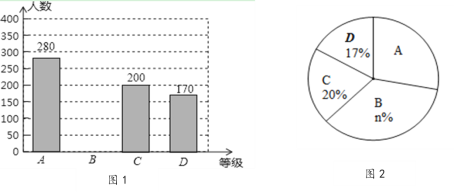
����(j��)�y(t��ng)Ӌ(j��)�D�ṩ����Ϣ���ش����І�(w��n)�}��
��1���@���{(di��o)��ČW(xu��)���˔�(sh��)�� �ˣ��D2�У�n= ��
��2�����νy(t��ng)Ӌ(j��)�D�У�ϲ��(��i)���Ї�(gu��)Ԋ(sh��)�~���(hu��)����(ji��)Ŀ����(du��)��(y��ng)���εĈA�Ľ��� �ȣ�
��3���a(b��)ȫ�D1�еėl�νy(t��ng)Ӌ(j��)�D��
��4������(j��)����{(di��o)��ĽY(ji��)����Ո(q��ng)���Ӌ(j��)ԓУ6000���W(xu��)�����ж��ٌW(xu��)��ϲ��(��i)���(qi��ng)���X����(ji��)Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D1������![]() �[����ƽ��ֱ������(bi��o)ϵ�У��c(di��n)
�[����ƽ��ֱ������(bi��o)ϵ�У��c(di��n)![]() ��
��![]() �S�ϣ��c(di��n)
�S�ϣ��c(di��n)![]() ��
��![]() �S�ϣ�
�S�ϣ�![]() ��
��![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��������
��ֱ��������![]() ��߅
��߅![]() ���c(di��n)
���c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ���c�c(di��n)
���c�c(di��n)![]() ��
��![]() �غϣ��^(gu��)�c(di��n)
�غϣ��^(gu��)�c(di��n)![]() ��
��![]() ��
��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ����
����![]() �S���c(di��n)
�S���c(di��n)![]() ��
��
��1����![]() �����ֱ�������Σ�
�����ֱ�������Σ�
����ֱ��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
����![]() �S������һ�c(di��n)
�S������һ�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��Ո(q��ng)?ji��n)�ֱ��
��Ո(q��ng)?ji��n)�ֱ��![]() ��
��![]() �S�Ϸքe��һ�c(di��n)
�S�Ϸքe��һ�c(di��n)![]() ��
��![]() ��ʹ
��ʹ![]() �����L(zh��ng)��С��������˕r(sh��)�c(di��n)
�����L(zh��ng)��С��������˕r(sh��)�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���L(zh��ng)����Сֵ��
���L(zh��ng)����Сֵ��
��2����D2���^(gu��)�c(di��n)![]() ��
��![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����c(di��n)����߅����ƽ����߅�Σ���ֱ��
����c(di��n)����߅����ƽ����߅�Σ���ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����(sh��)�S���Ѓɶ��c(di��n)A��B���c(di��n)![]() ��ʾ�Ĕ�(sh��)��6���c(di��n)B���c(di��n)A�����(c��)����AB=20����(d��ng)�c(di��n)P���c(di��n)A���l(f��)����ÿ��4��(g��)��λ�L(zh��ng)�ȵ��ٶ���?c��i)?sh��)�S��������\(y��n)��(d��ng)���O(sh��)�\(y��n)��(d��ng)�r(sh��)�g��t�루t>0��.
��ʾ�Ĕ�(sh��)��6���c(di��n)B���c(di��n)A�����(c��)����AB=20����(d��ng)�c(di��n)P���c(di��n)A���l(f��)����ÿ��4��(g��)��λ�L(zh��ng)�ȵ��ٶ���?c��i)?sh��)�S��������\(y��n)��(d��ng)���O(sh��)�\(y��n)��(d��ng)�r(sh��)�g��t�루t>0��.
![]()
��1����(xi��)����(sh��)�S���c(di��n)B��ʾ�Ĕ�(sh��)______���c(di��n)P��ʾ�Ĕ�(sh��)�ú�t��ʽ�ӱ�ʾ��_______��
��2���O(sh��)�c(di��n)M��AP�����c(di��n)���c(di��n)N��PB�����c(di��n).�c(di��n)P��ֱ��AB���\(y��n)��(d��ng)���^(gu��)���У�����MN���L(zh��ng)���Ƿ��(hu��)�l(f��)��׃�������l(f��)��׃����Ո(q��ng)�f(shu��)�����ɣ�����׃�����������MN���L(zh��ng)��.
��3����(d��ng)�c(di��n)R���c(di��n)B���l(f��)����ÿ��2��(g��)��λ�L(zh��ng)�ȵ��ٶ���?c��i)?sh��)�S��������\(y��n)��(d��ng)�����c(di��n)P��Rͬ�r(sh��)���l(f��)����(d��ng)�c(di��n)P�\(y��n)��(d��ng)������r(sh��)���c�c(di��n)R�ľ��x��2��(g��)��λ�L(zh��ng)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����һ�����ǰ��еăɉKֱ�ǰ��еăɂ�(g��)ֱ����c(di��n)�غ���һ�𣬼�����D��ʾ�ķ�ʽ�B����һ�����С�A��60�㣬��B��30����D��45�㣮
��1������BCD��45�㣬���ACE�ĶȔ�(sh��)��
��2������ACE��150�㣬���BCD�ĶȔ�(sh��)��
��3���ɣ�1������2�������ACE�c��BCD����ʲô�ӵĔ�(sh��)���P(gu��n)ϵ���f(shu��)�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���҂�Ҏ(gu��)��:���P(gu��n)��![]() ��һԪһ�η���
��һԪһ�η���![]() �Ľ��
�Ľ��![]() ���t�Q(ch��ng)ԓ���̞顰�ͽⷽ�̡�������:����
���t�Q(ch��ng)ԓ���̞顰�ͽⷽ�̡�������:����![]() �Ľ��
�Ľ��![]() ����
����![]() �� �t����
�� �t����![]() �顰�ͽⷽ��"��Ո(q��ng)����(j��)����Ҏ(gu��)��������І�(w��n)�}:(1)��֪�P(gu��n)��
�顰�ͽⷽ��"��Ո(q��ng)����(j��)����Ҏ(gu��)��������І�(w��n)�}:(1)��֪�P(gu��n)��![]() ��һԪһ�η���
��һԪһ�η���![]() �ǡ��ͽⷽ�̡����t
�ǡ��ͽⷽ�̡����t![]() ��ֵ��________��(2)��֪�P(gu��n)��
��ֵ��________��(2)��֪�P(gu��n)��![]() ��һԪһ�η���
��һԪһ�η���![]() �ǡ��ͽⷽ�̡����������Ľ���
�ǡ��ͽⷽ�̡����������Ľ���![]() ���t
���t![]() ��ֵ��_________��
��ֵ��_________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����x���ϣ�
����1����һԪ���η���ax2+bx+c=0��a��0���ăɸ���x1��x2���tx1+x2=![]() ��x1x2=
��x1x2=![]() ��
��
����2����֪��(sh��)��(sh��)m��n�M��m2��m��1=0��n2��n��1=0����m��n����![]() ��ֵ��
��ֵ��
�⣺���}֪m��n�Ƿ���x2��x��1=0�ăɂ�(g��)����ȵČ�(sh��)��(sh��)��������(j��)����1��
m+n=1��mn=��1
��![]()
����(j��)�������Ͻ�Q���憖(w��n)�}��
��1��һԪ���η���2x2+3x��1=0�ăɸ���x1��x2���tx1+x2=�� ����x1x2=�� ����
��2����֪��(sh��)��(sh��)m��n�M��2m2��2m��1=0��2n2��2n��1=0����m��n����m2n+mn2��ֵ��
��3����֪��(sh��)��(sh��)p��q�M��p2=3p+2��2q2=3q+1����p��2q����p2+4q2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵxOy�У���һ���タ����_(d��)ʽ��![]() .
.
��1����(d��ng)ԓ���タ�^(gu��)ԭ�c(di��n)�r(sh��)����![]() ��ֵ��
��ֵ��
��2������(bi��o)ϵ��(n��i)��һ����OABC,����![]() ��
��![]() .
.
��ֱ�ӌ�(xi��)��C�c(di��n)����(bi��o)��
��������タ![]() �cԓ������2��(g��)���c(di��n)����
�cԓ������2��(g��)���c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����タy=x2+bx+c�Č�(du��)�Q(ch��ng)�S��ֱ��x=1��ԓ���タ�cx�S�ăɂ�(g��)���c(di��n)�քe��A��B���cy�S�Ľ��c(di��n)��C������A��-1��0��.
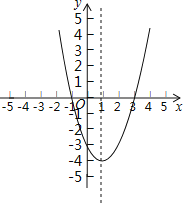
��1����(xi��)��B�c(di��n)������(bi��o) ��
��2�����タ�ĺ���(sh��)����ʽ��
��3�������タ�ϴ���һ�c(di��n)P��ʹ����POC����e����BOC����e��2�������c(di��n)P������(bi��o)��
��4���c(di��n)M�Ǿ���BC��һ�c(di��n)���^(gu��)�c(di��n)M��x�S�Ĵ��������タ���c(di��n)D����MD�L(zh��ng)�ȵ����ֵ��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com