【題目】隨著生活水平的提高，人們對空氣質量的要求也越來越高。為了了解
月中旬長春市城區的空氣質量情況，某校“綜合實踐環境調查”小組，從天氣預報網抽取了朝陽區和南關區這兩個城區
年月
日——年月
日的空氣質量指數，作為樣本進行統計，過程如下，請補充完整.
收集數據
朝陽區 |
|
|
|
|
|
|
|
|
|
|
南關區 |
|
|
|
|
|
|
|
|
|
|
整理、描述數據
按下表整理、描述這兩城區空氣質量指數的數據.
空氣質量 | 優 | 良 | 輕微污染 | 中度污染 | 重度污染 |
朝陽區 | |||||
南關區 |
|
|
|
|
|
（說明：空氣質量指數
時，空氣質量為優；
空氣質量指數
時，空氣質量為良；
空氣質量指數
時，空氣質量為輕微污染；
空氣質量指數
時，空氣質量為中度污染；
空氣質量指數
時，空氣質量為重度污染.）
分析數據
兩城區的空氣質量指數的平均數、中位數、方差如下表所示.
城區 | 平均數 | 中位數 | 方差 |
朝陽區 |
|
|
|
南關區 |
|
|
請將以上兩個表格補充完整.
得出結論可以推斷出哪個城區這十天中空氣質量情況比較好？請至少從兩個不同的角度說明推斷的合理性.
【答案】整理、描述數據見表格；分析數據見表格；得出結論：南關區這十天中空氣質量情況比較好.理由見解析.
【解析】
數出朝陽區空氣質量指數在各個范圍的天數即可填出第一個表格；將南關區空氣質量指數按照從小到大的順序排列，中間兩個位置的數據的平均數即為中位數；根據表格中的數據，結合平均數、中位數對數據進行分析即可．
解：整理、描述數據
空氣質量 | 優 | 良 | 輕微污染 | 中度污染 | 重度污染 |
朝陽區 |
|
|
|
|
|
南關區 |
|
|
|
|
|
分析數據
城區 | 平均數 | 中位數 | 方差 |
朝陽區 |
|
|
|
南關區 |
|
|
|
得出結論：南關區這十天中空氣質量情況比較好;
理由：這十天南關區空氣質量優的天數多于朝陽區，同時南關區的污染指數的平均數和中位數均小于朝陽區的，因此南關區這十天中空氣質量情況比較好.
科目：初中數學 來源： 題型：
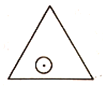
【題目】如圖，一個半徑為
的圓形紙片在邊長為
的等邊三角形內任意運動，則在該等邊三角形內，這個圓形紙片“不能接觸到的部分”的面積是____________.
查看答案和解析>>
科目：初中數學 來源： 題型：
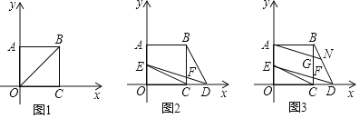
【題目】如圖，矩形ABCO在平面直角坐標系中，AO，CO分別在y軸，x軸正半軸上，若S矩形AOCB=
BO2，矩形AOCB的周長為16．
（1）求B點坐標；
（2）點D在OC延長線上，設D點橫坐標為d，連BD，將直線DB繞D點逆時針方向旋轉45°交AO于E，交BC于F，連EC，設△CDE面積=S，求出S與d的函數關系式并注明自變量d的取值范圍；
（3）在（2）條件下，當點E在AO上時，過A作ED的平行線交CB于G，交BD于N，若BG=2CF，求S的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
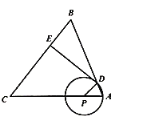
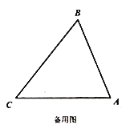
【題目】如圖，在
中，
，
,點
是
邊上一動點（不與點
重合），以
長為半徑的
與邊
的另一個交點為
，過點作
于點
.
當與邊相切時，求的半徑；
聯結
交
于點
，設
的長為
，
的長為
，求關于的函數解析式，并直接寫出的取值范圍；
在的條件下，當以
長為直徑的
與相交于
邊上的點
時，求相交所得的公共弦的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】畫出二次函數y=2x2+8x+6的圖象．
（1）根據圖象寫出當y隨x的增大而減小時x的范圍；
（2）根據圖象寫出滿足不等式2x2+8x+6＜0的x的取值范圍；
（3）求函數圖象與兩坐標軸交點所圍成的三角形的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在多項式的乘法公式中，完全平方公式
是其中重要的一個.
（1）請補全完全平方公式的推導過程：
，
，
.
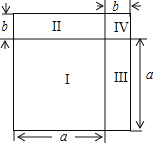
（2）如圖，將邊長為
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分，請你結合圖給出完全平方公式的幾何解釋.
（3）用完全平方公式求
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，
，以點
為圓心、2為半徑畫圓，點
是
上任意一點，連接
，
.將繞點按順時針方向旋轉
，交于點
，連接
（1）當與相切時，
①求證：是的切線；
②求點到
的距離.
（2）連接
，
，當
的面積最大時，點
到的距離為 .
查看答案和解析>>
科目：初中數學 來源： 題型：
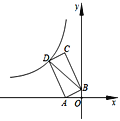
【題目】如圖，點A(－2，0)，B(0，1)，以線段AB為邊在第二象限作矩形ABCD，雙曲線
(k<0)經過點D，連接BD，若四邊形OADB的面積為6，則k的值是_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
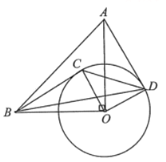
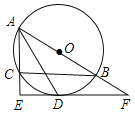
【題目】如圖，⊙O是△ABC的外接圓，AB為直徑，∠BAC的平分線交⊙O于點D，過點D作DE⊥AC分別交AC、AB的延長線于點E、F．
（1）求證：EF是⊙O的切線；
（2）若AC=4，CE=2，求
的長度．（結果保留π）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
