

 的位置.
的位置. 的過程中邊PA所掃過區域 (圖甲中陰影部分)的面積;
的過程中邊PA所掃過區域 (圖甲中陰影部分)的面積;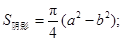 ②6;(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,由勾股逆定理證出∠
②6;(2)將△PAB繞點B順時針旋轉90°到△P′CB的位置,由勾股逆定理證出∠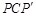 =90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
=90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.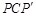 =90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.
=90°,再證∠BPC+∠APB=180°,即點P在對角線AC上.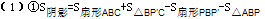
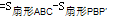
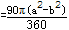
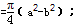

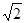 ,P′C=PA=2,根據勾股定理可得PC=6.
,P′C=PA=2,根據勾股定理可得PC=6.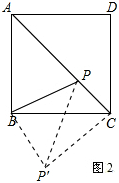


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:初中數學 來源:不詳 題型:解答題

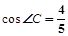 ,求⊙O的直徑.
,求⊙O的直徑.查看答案和解析>>
科目:初中數學 來源:不詳 題型:計算題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
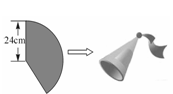
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
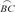 的中點,DE垂直于AC的延長線于E,連結BC,若DE=6cm,CE=2cm,下列結論錯誤的是( )
的中點,DE垂直于AC的延長線于E,連結BC,若DE=6cm,CE=2cm,下列結論錯誤的是( )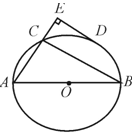
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
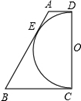
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com