
【題目】已知:如圖①,將![]() 的菱形
的菱形![]() 沿對(duì)角線
沿對(duì)角線![]() 剪開(kāi),將
剪開(kāi),將![]() 沿射線
沿射線![]() 方向平移,得到
方向平移,得到![]() 點(diǎn)
點(diǎn)![]() 為邊
為邊![]() 上一點(diǎn)(點(diǎn)
上一點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 重合),將射線
重合),將射線![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,與
,與![]() 的延長(zhǎng)線交于點(diǎn)
的延長(zhǎng)線交于點(diǎn)![]() ,連接
,連接![]() .
.
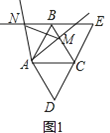
![]() ①求證:
①求證:![]() ;
;
②探究![]() 的形狀;
的形狀;
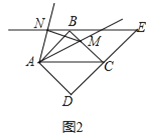
![]() 如圖②,若菱形
如圖②,若菱形![]() 變?yōu)檎叫?/span>
變?yōu)檎叫?/span>![]() ,將射線
,將射線![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,原題其他條件不變,
,原題其他條件不變,![]() 中的①和②兩個(gè)結(jié)論是否仍然成立?若成立,請(qǐng)直接寫出結(jié)論;若不成立,請(qǐng)寫出變化后的結(jié)論并證明.
中的①和②兩個(gè)結(jié)論是否仍然成立?若成立,請(qǐng)直接寫出結(jié)論;若不成立,請(qǐng)寫出變化后的結(jié)論并證明.
【答案】(1)①證明見(jiàn)解析;②△![]() 是等邊三角形,理由見(jiàn)解析;(2)①∠
是等邊三角形,理由見(jiàn)解析;(2)①∠![]() =∠
=∠![]() 成立,理由見(jiàn)解析;②不成立,△
成立,理由見(jiàn)解析;②不成立,△![]() 是等腰直角三角形,理由見(jiàn)解析.
是等腰直角三角形,理由見(jiàn)解析.
【解析】
(1)①先由菱形可知四邊相等,再由∠D=60°得等邊△ADC和等邊△ABC,則對(duì)角線AC與四邊都相等,利用ASA證明△ANB≌△AMC,得結(jié)論;
②根據(jù)有一個(gè)角是60°的等腰三角形是等邊三角形得出:△AMN是等邊三角形;
(2)①成立,根據(jù)正方形得45°角和射線AM繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)45°,證明△ANB∽△AMC,得∠ANB=∠AMC;
②不成立,△AMN是等腰直角三角形,利用①中的△ANB∽△AMC,得比例式進(jìn)行變形后,再證明△NAM∽△BAD,則△AMN是等腰直角三角形.
(1)如圖1,①∵四邊形![]() 是菱形,
是菱形,

∴![]() ,
,
∵∠![]()
![]() 60°,
60°,
∴△ADC和△ABC是等邊三角形,
∴![]() ,∠BAC
,∠BAC![]() 60°,
60°,
∵∠![]()
![]() 60°,
60°,
∴∠![]() =∠
=∠![]() ,
,
由△ADC沿射線DC方向平移得到△BCE,可知∠CBE![]() 60°,
60°,
∵∠ABC![]() 60°,
60°,
∴∠ABN![]() 60°,
60°,
∴∠ABN![]() ∠ACB
∠ACB![]() 60°
60°
∴△![]() ≌△
≌△![]() ,
,
∴∠![]() =∠
=∠![]() ;
;
②如圖1,△![]() 是等邊三角形,理由是:
是等邊三角形,理由是:
由△![]() ≌△
≌△![]() ,
,
∴AM![]() AN,
AN,
∵∠![]()
![]() 60°,
60°,
∴△![]() 是等邊三角形;
是等邊三角形;
(2)①如圖2,∠![]() =∠
=∠![]() 成立,理由是:
成立,理由是:

在正方形ABCD中,
∴∠BAC![]() ∠DAC=∠BCA
∠DAC=∠BCA![]() 45°,
45°,
∵∠NAM![]() 45°,
45°,
∴∠![]() =∠
=∠![]() ,
,
由平移得:∠EBC![]() ∠CAD
∠CAD![]() 45°,
45°,
∵∠ABC=90°,
∴∠ABN![]() 180°
180°![]() 90°45°
90°45°![]() 45°,
45°,
∴∠ABN![]() ∠ACM
∠ACM![]() 45°,
45°,
∴△![]() ∽△
∽△![]() ,
,
∴∠![]() =∠
=∠![]() ;
;
②如圖2,不成立,
△![]() 是等腰直角三角形,理由是:
是等腰直角三角形,理由是:
∵△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠![]() =∠
=∠![]() =45°,
=45°,
∴△![]() ∽△
∽△![]() ,
,
∴∠![]() =∠
=∠![]() =90°,
=90°,
∴△![]() 是等腰直角三角形.
是等腰直角三角形.


 狀元坊全程突破導(dǎo)練測(cè)系列答案
狀元坊全程突破導(dǎo)練測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,A點(diǎn)的坐標(biāo)為(﹣1,5),B點(diǎn)的坐標(biāo)為(3,3),C點(diǎn)的坐標(biāo)為(5,3),D點(diǎn)的坐 標(biāo)為(3,﹣1),小明發(fā)現(xiàn):線段AB與線段CD存在一種特殊關(guān)系,即其中一條線段繞著某點(diǎn)旋轉(zhuǎn)一個(gè)角度可以得到另一條線段,你認(rèn)為這個(gè)旋轉(zhuǎn)中心的坐標(biāo)是_____________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
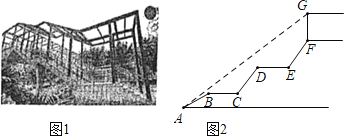
【題目】為了方便學(xué)生在上下學(xué)期間安全過(guò)馬路,南岸區(qū)政府決定在南開(kāi)(融僑)中學(xué)校門口修建人行天橋(如圖1),其平面圖如圖2所示,初三(8)班的學(xué)生小劉想利用所學(xué)知識(shí)測(cè)量天橋頂棚距地面的高度.天橋入口A點(diǎn)有一臺(tái)階AB=2m,其坡角為30°,在AB上方有兩段平層BC=DE=1.5m,且BC,DE與地面平行,BC,DE上方又緊接臺(tái)階CD,EF,其長(zhǎng)度相等且坡度均為i=4:3,頂棚距天橋距離FG=2m,且小劉從入口A點(diǎn)測(cè)得頂棚頂端G的仰角為37°,請(qǐng)根據(jù)以上數(shù)據(jù),幫小劉計(jì)算出頂端G點(diǎn)距地面高度為( )m.(結(jié)果保留一位小數(shù),參考數(shù)據(jù):![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
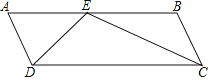
【題目】如圖,在平行四邊形ABCD中,∠B=120°,AB與CD之間的距離是![]() ,AB=28,在AB上取一點(diǎn)E(AE<BE),使得∠DEC=120°,則AE=_____.
,AB=28,在AB上取一點(diǎn)E(AE<BE),使得∠DEC=120°,則AE=_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
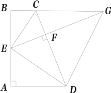
【題目】如圖,已知四邊形ABCD中,AB⊥AD,BC∥AD,E為AB的中點(diǎn),且EC、ED分別為∠BCD、∠ADC的角平分線,EF⊥CD交BC的延長(zhǎng)線于點(diǎn)G,連接DG.
(1)求證:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)當(dāng)△BCE與△DFG相似時(shí),![]() 的值是 .
的值是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在菱形ABCD中,AB=2,∠DAB=60°,點(diǎn)E是AD邊的中點(diǎn),點(diǎn)M是AB邊上的一個(gè)動(dòng)點(diǎn)(不與點(diǎn)A重合),延長(zhǎng)ME交CD的延長(zhǎng)線于點(diǎn)N,連接MD,AN.
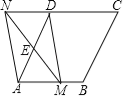
(1)求證:四邊形AMDN是平行四邊形.
(2)當(dāng)AM的值為何值時(shí),四邊形AMDN是矩形?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】4張相同的卡片上分別寫有數(shù)字1、2、3、4,將卡片背面朝上,洗勻后從中任意抽取1張,將卡片上的數(shù)字作為被減數(shù);一只不透明的袋子中裝有標(biāo)號(hào)為1、2、3的3個(gè)小球,這些球除標(biāo)號(hào)外都相同,攪勻后從中任意摸出1個(gè)球,將摸到的球的標(biāo)號(hào)作為減數(shù).
(1)求這兩個(gè)數(shù)的差為0的概率;
(2)游戲規(guī)則規(guī)定:當(dāng)抽到的這兩個(gè)數(shù)的差為非負(fù)數(shù)時(shí),甲獲勝;否則,乙獲勝.這樣的規(guī)則公平嗎?如果不公平,請(qǐng)?jiān)O(shè)計(jì)一個(gè)公平的規(guī)則,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
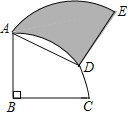
【題目】如圖,將半徑為4,圓心角為90°的扇形BAC繞A點(diǎn)逆時(shí)針旋轉(zhuǎn)60°,點(diǎn)B、C的對(duì)應(yīng)點(diǎn)分別為點(diǎn)D、E且點(diǎn)D剛好在![]() 上,則陰影部分的面積為_____.
上,則陰影部分的面積為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
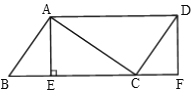
【題目】如圖,在平行四邊形ABCD中,AE⊥BC于E,點(diǎn)F在BC延長(zhǎng)線上,且CF=BE,連接AC,DF,
(1)求證:四邊形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的長(zhǎng)度.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com