
【題目】已知正比例函數y=kx經過點A,點A在第四象限,過點A作AH⊥x軸,垂足為點H,點A的橫坐標為3,且△AOH的面積為3.
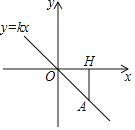
(1)求正比例函數的表達式;
(2)在x軸上能否找到一點M,使△AOM是等腰三角形?若存在,求點M的坐標;若不存在,請說明理由.
【答案】(1)y=﹣![]() x;(2)當點M的坐標為(﹣
x;(2)當點M的坐標為(﹣![]() ,0)、(
,0)、(![]() ,0)、(6,0)或(
,0)、(6,0)或(![]() ,0)時,△AOM是等腰三角形.
,0)時,△AOM是等腰三角形.
【解析】
(1)根據點A的橫坐標、△AOH的面積結合點A所在的象限,即可得出點A的坐標,再利用待定系數法即可求出正比例函數的表達式;
(2)分OM=OA、AO=AM、OM=MA三種情況考慮,①當OM=OA時,根據點A的坐標可求出OA的長度,進而可得出點M的坐標;②當AO=AM時,由點H的坐標可求出點M的坐標;③當OM=MA時,設OM=x,則MH=3﹣x,利用勾股定理可求出x值,進而可得出點M的坐標.綜上即可得出結論.
解:(1)∵點A的橫坐標為3,△AOH的面積為3,點A在第四象限,
∴點A的坐標為(3,﹣2).
將A(3,﹣2)代入y=kx,
﹣2=3k,解得:k=﹣![]() ,
,
∴正比例函數的表達式為y=﹣![]() x.
x.
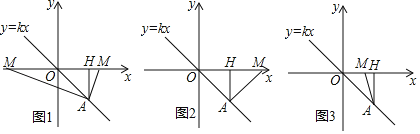
(2)①當OM=OA時,如圖1所示,
∵點A的坐標為(3,﹣2),
∴OH=3,AH=2,OA=![]() =
=![]() ,
,
∴點M的坐標為(﹣![]() ,0)或(
,0)或(![]() ,0);
,0);
②當AO=AM時,如圖2所示,
∵點H的坐標為(3,0),
∴點M的坐標為(6,0);
③當OM=MA時,設OM=x,則MH=3﹣x,
∵OM=MA,
∴x=![]() ,
,
解得:x=![]() ,
,
∴點M的坐標為(![]() ,0).
,0).
綜上所述:當點M的坐標為(﹣![]() ,0)、(
,0)、(![]() ,0)、(6,0)或(
,0)、(6,0)或(![]() ,0)時,△AOM是等腰三角形.
,0)時,△AOM是等腰三角形.


 優學名師名題系列答案
優學名師名題系列答案科目:初中數學 來源: 題型:
【題目】把所有正偶數從小到大排列,并按如下規律分組:(2)、(4,6),(8,10,12),(14,16,18,20),…,現有等式Am=(i,j)表示正偶數m是第i組第j個數(從左往右數).如A2=(1,1),A10=(3,2),A18=(4,3),則A200可表示為( )
A.(14,9)B.(14,10)C.(15,9)D.(15,10)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.如果一個圖形是中心對稱圖形,那么它一定不是軸對稱圖形
B.正方形是軸對稱圖形,它共有兩條對稱軸
C.等邊三角形是旋轉對稱圖形,它的最小旋轉角等于![]() 度
度
D.平行四邊形是中心對稱圖形,其對稱中心是它的一條對角線的中點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AB∥CD.∠1=∠2,∠3=∠4,試說明AD∥BE.
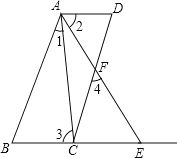
解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,水壩的橫截面是梯形ABCD,∠ABC=37°,壩頂DC=3m,背水坡AD的坡度i(即tan∠DAB)為1:0.5,壩底AB=14m.
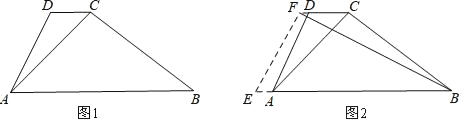
(1)求壩高;
(2)如圖2,為了提高堤壩的防洪抗洪能力,防汛指揮部決定在背水坡將壩頂和壩底間時拓寬加固,使得AE=2DF,EF⊥BF,求DF的長.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,一次函數y=![]() x+3的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.
x+3的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.

(1)直線CD的函數表達式為 ;(直接寫出結果)
(2)點Q為線段DE上的一個動點,連接BQ.
①若直線BQ將△BDE的面積分為1:2兩部分,試求點Q的坐標;
②點Q是否存在某個位置,將△BQD沿著直線BQ翻折,使得點D恰好落在直線AB下方的坐標軸上?若存在,求點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
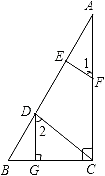
【題目】已知:如圖,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求證:CD⊥AB.
證明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定義)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代換)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
查看答案和解析>>
科目:初中數學 來源: 題型:
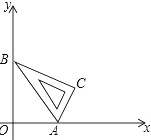
【題目】如圖,將含有30°角的直角三角板ABC放入平面直角坐標系,頂點A,B分別落在x、y軸的正半軸上,∠OAB=60°,點A的坐標為(1,0),將三角板ABC沿x軸向右作無滑動的滾動(先繞點A按順時針方向旋轉60°,再繞點C按順時針方向旋轉90°,…)當點B第一次落在x軸上時,則點B運動的路徑與坐標軸圍成的圖形面積是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市居民使用自來水按如下標準收費(水費按月繳納)
月用水量 | 單價 |
不超過 |
|
超過 |
|
超過 |
|
(1)當![]() 時,某用戶用了
時,某用戶用了![]() 水,求該用戶這個月應該繳納的水費;
水,求該用戶這個月應該繳納的水費;
(2)設某用戶用水量為![]() 立方米,求該用戶應繳納的水費(用含
立方米,求該用戶應繳納的水費(用含![]() 的式子表達)
的式子表達)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com