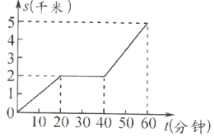
【題目】甲、乙兩人同時從A地前往相距5千米的B地.甲騎自行車，途中修車耽誤了20分鐘，甲行駛的路程
（千米）關于時間
（分鐘）的函數圖像如圖所示；乙慢跑所行的路程（千米）關于時間（分鐘）的函數解析式為
.
（1）在圖中畫出乙慢跑所行的路程關于時間的函數圖像；
（2）乙慢跑的速度是每分鐘________千米；
（3）甲修車后行駛的速度是每分鐘________千米；
（4）甲、乙兩人在出發后，中途________分鐘時相遇.
【答案】（1）圖像見解析；（2）
；（3）
；（4）24.
【解析】
（1）根據所給解析式可知函數過原點，并過點（60，5），由這兩點即可得出答案．
（2）乙慢跑的速度即是乙慢跑所行的路程s（千米）關于時間t（分鐘）的函數解析式的斜率；
（3）甲修車后行駛路程是3km，所用時間是20min，即可求出速度；
（4）甲乙相遇，體現在（1）中的圖形即是它們的交點，即求出交點得出答案．
（1）所畫圖形如下所示：
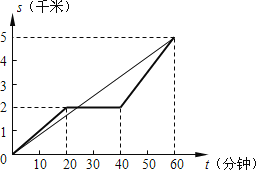
（2）乙慢跑的速度為:
千米/分鐘；
（3）甲修車后行駛20min，所形路程為3km，
故甲修車后行駛的速度為：3÷20=km/min；
（4）由甲行駛的路程s（千米）關于時間t（分鐘）的函數圖象與乙慢跑所行的路程s（千米）關于時間t（分鐘）的函數圖象可知：
在距離A地2km處甲乙相遇，此時乙行駛了2×12=24分鐘，
即甲、乙兩人在出發后，中途24分鐘時相遇．
王后雄學案教材完全解讀系列答案
海淀課時新作業金榜卷系列答案科目：初中數學 來源： 題型：
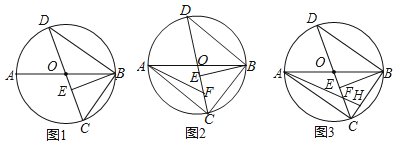
【題目】如圖，AB、CD是
的直徑，
于E，連接BD．
如圖1，求證：
；
如圖2，F是OC上一點，
，求證：
；
在的條件下，連接BC，AF的延長線交BC于H，若
，
，求HF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分線與AB的垂直平分線交于點O，將∠C沿EF（E在BC上，F在AC上）折疊，點C與點O恰好重合，則∠OEC為 度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線的頂點為A（1，4），拋物線與y軸交于點B（0，3），與x軸交于C、D兩點．點P是x軸上的一個動點．
（1）求此拋物線的解析式；
（2）求C、D兩點坐標及△BCD的面積；
（3）若點P在x軸上方的拋物線上，滿足S△PCD=
S△BCD，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在矩形ABCD中，AB=4cm，BC=8cm,動點P從點A出發，以1cm/s的速度沿AB向點B運動，動點Q從點B出發，以2cm/s秒的速度沿BC向點C運動.P、Q分別從A、B同時出發，設運動時間為t秒.(如圖1)
（１）用含t的代數式表示下列線段長度：
①PB=__________cm,②QB=_____cm,③CQ=_________cm.
(2)當△PBQ的面積等于3
時，求t的值.
(3) (如圖2)，若E為邊CD中點，連結EQ、AQ.當以A、B、Q為頂點的三角形與△EQC相似時，直接寫出滿足條件的t的所有值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，點F，C是⊙O上兩點，且
，連接AC，AF，過點C作CD⊥AF交AF延長線于點D，垂足為D．
(1)求證：CD是⊙O的切線；
(2)若CD=2
，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 如圖，在平面直角坐標系中，點O坐標原點，直線l分別交x軸、y軸于A，B兩點，OA＜OB，且OA、OB的長分別是一元二次方程
的兩根．
（1）求直線AB的函數表達式；
（2）點P是y軸上的點，點Q第一象限內的點．若以A、B、P、Q為頂點的四邊形是菱形，請直接寫出Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，正方形ABCD的邊長為4，把三角板的直角頂點放置BC中點E處，三角板繞點E旋轉，三角板的兩邊分別交邊AB、CD于點G、F．
（1）求證：△GBE∽△GEF．
（2）設AG=x，GF=y，求Y關于X的函數表達式，并寫出自變量取值范圍．
（3）如圖2，連接AC交GF于點Q，交EF于點P．當△AGQ與△CEP相似，求線段AG的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com