
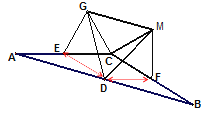
【題目】已知,如圖,在![]() 中,AC=BC,點D是邊AB的中點,E,F分別是AC和BC的中點,分別以CE,CF為一邊向上作兩個全等的矩形CEGH和矩形CFMN(其中EG=FM),依次連結DG、DM、GM。
中,AC=BC,點D是邊AB的中點,E,F分別是AC和BC的中點,分別以CE,CF為一邊向上作兩個全等的矩形CEGH和矩形CFMN(其中EG=FM),依次連結DG、DM、GM。
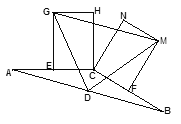
(1)求證:![]() 是等腰三角形。
是等腰三角形。
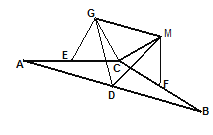
(2)如圖,若將上圖中的兩個全等的矩形改為兩個全等的正三角形(![]() 和
和![]() ),其他條件不變。請探究
),其他條件不變。請探究![]() 的形狀,并說明理由。
的形狀,并說明理由。
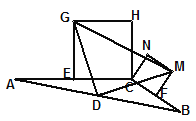
(3)若將上圖中的兩個全等的矩形改為兩個正方形,并把![]() 中的邊BC縮短到如圖形狀,請探究
中的邊BC縮短到如圖形狀,請探究![]() 的形狀,并說明理由。
的形狀,并說明理由。
【答案】(1)證明見解析 (2)△DGM是等邊三角形. (3)△DGM是等腰直角三角形.
【解析】試題分析:(1)先根據SAS證明△FBM≌△MDH,得到DG=DM,即![]() 是等腰三角形;(2)類似先證
是等腰三角形;(2)類似先證![]() 是等腰三角形,再求GM=GD,從而得出
是等腰三角形,再求GM=GD,從而得出![]() 是等邊三角形;(3)類似(1)(2)中方法,先得到
是等邊三角形;(3)類似(1)(2)中方法,先得到![]() 是等腰三角形,再求∠GDM=∠GEC=900,從而得出
是等腰三角形,再求∠GDM=∠GEC=900,從而得出![]() 是等腰直角三角形;
是等腰直角三角形;
試題解析:
(1)證明:∵四邊形CEGH和CFMN是全等的矩形,
∴CE= CF,EG=FM,∠GEC =∠MFC = 90°.
連接DE、DF,如圖.
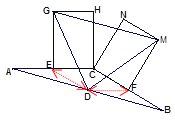
∵D、E、F分別是AB、AC、BC的中點,
DE∥BC,且DE=CE =![]() BC;
BC;
DF∥AC,且DF = CE = ![]() AC.
AC.
∴四邊形DECF是平行四邊形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,
∴∠DEG=∠DFM.
∵AC=BC,
∴DE=DF.
∴△FBM≌△MDH(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
(2)△DGM是等邊三角形.
證明:∵![]() 和
和![]() 是全等的等邊三角形,
是全等的等邊三角形,
∴CE=EG=CG=CF=FM=CM,∠GEC=∠MFC=60°.
連接DE、DF,如圖.
∵D、E、F分別是AB、AC、BC的中點,
∴DE∥BC,且DE =CE =![]() BC;
BC;
DF∥AC,且DF=CE=![]() AC.
AC.
∴四邊形DECF是平行四邊形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,
∴∠DEG=∠DFM.
∵AC=BC,
∴DE=DF.
∴△FBM≌△MDH(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
又∵∠GCM+∠ACB=3600-600-600=2400
∠GED+∠ACB=∠GEC+∠CED+∠ACB=600+1800=2400
∴∠GCM=∠GED
又DE=CF=CM,EG=CG
∴△GED≌△GCM(SAS).
∴GM=GD
∴△DGM是等邊三角形.
(3)△DGM是等腰直角三角形.
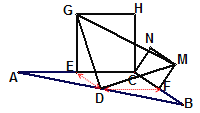
顯然,由(1)(2)易得△GED≌△DFM(SAS)
∴DG=DM,∠DGE=∠MDF
∵DF∥AC
∴∠CED+∠EDF=1800/p>
即:∠CED+∠EDG+∠GDM+∠MDF=1800
又由三角形內角和可知∠CED+∠EDG+∠GEC+∠DGE=1800
∴∠GDM=∠GEC=900
∴△DGM是等腰直角三角形.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案科目:初中數學 來源: 題型:
【題目】體育課上,某班兩名同學分別進行了5次短跑訓練,要判斷哪一名同學的成績比較穩定,通常需要比較兩名同學成績的( )
A. 平均數 B. 方差 C. 頻數分布 D. 中位數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據農業農村部新聞部辦公室2018年10月15日消息,江寧省發現疑似非洲豬瘟疫情,此次豬瘟疫情發病急,蔓延速度快.當政府和企業迅速進行了豬瘟疫情排査和處置.在疫情排査過程中.某農場第一天發現3頭生豬發病.兩天后發現共有363頭生豬發病,求每頭發病生豬平均每天傳染多少頭生豬?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ΔABC中,∠ABC和∠ACB的平分線交于點E,過點E作MN∥BC交AB于M, 交AC于N,若BM+CN=9,則線段MN的長為( )
A.6
B.7
C.8
D.9
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com