Question

【題目】在平面直角坐標系中，已知直線y＝﹣x+4與x軸、y軸分別交于A、B兩點，點C(0，n)是y軸上一點．把坐標平面沿直線AC折疊，使點B剛好落在x軸上，則點C的坐標為______．

Answer 1

【答案】(0，1.5)或(0，﹣6)

【解析】

分兩種情況討論：①當B′在x軸負半軸上時，過C作CD⊥AB于D，先求出A，B的坐標，分別為（3，0），（0，4），得到AB的長，再根據折疊的性質得到AC平分∠OAB，得到CD=CO=n，DA=OA=3，則DB=5-3=2，BC=4-n，在Rt△BCD中，利用勾股定理得到n的方程，解方程求出n即可．②當B'在x軸正半軸上時，設OC=x，在Rt△OCB′中，利用勾股定理可求出x的值．

①若B′在x軸左半軸，過C作CD⊥AB于D，如圖1，

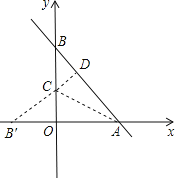
對于直線，令x=0，得y=4；令y=0，x=3，

∴A(3,0),B(0,4)，即OA=3，OB=4，

∴AB=5，

又∵坐標平面沿直線AC折疊，使點B剛好落在x軸上，

∴AC平分∠OAB，

∴CD=CO=n，則BC=4n，

∴DA=OA=3，

∴DB=53=2，

在Rt△BCD中,

∴解得n=1.5，

∴點C的坐標為(0,1.5).

②若B′在x軸右半軸，如圖，

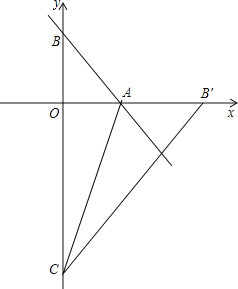
則AB′=AB=5，

設OC=x,則CB′=CB=x+4,OB′=OA+AB′=3+5=8，

在Rt△OCB′中, ,即

解得：x=6,即可得此時點C的坐標為(0,6).

故答案為：(0,1.5)或(0,6).