
【題目】已知邊長為2的正六邊形ABCDEF在平面直角坐標系中的位置如圖所示,點B在原點,把正六邊形ABCDEF沿x軸正半軸作無滑動的連續翻轉,每次翻轉60°,經過2018次翻轉之后,點B的坐標是______.

【答案】(4033,![]() )
)
【解析】
根據正六邊形的特點,每6次翻轉為一個循環組循環,用2018除以6,根據商和余數的情況確定出點B的位置,經過第2017次翻轉之后,點B的位置不變,仍在x軸上,由A(﹣2,0),可得AB=2,即可求得點B離原點的距離為4032,所以經過2017次翻轉之后,點B的坐標是(4032,0),經過2018次翻轉之后,點B在B′位置(如圖所示),則△BB′C為等邊三角形,可求得BN=NC=1,B′N=![]() ,由此即可求得經過2018次翻轉之后點B的坐標.
,由此即可求得經過2018次翻轉之后點B的坐標.
然后求出翻轉前進的距離,過點C作CG⊥x于G,求出∠CBG=60°,然后求出CG、BG,再求出OG,然后寫出點C的坐標即可.
設2018次翻轉之后,在B′點位置,
∵正六邊形ABCDEF沿x軸正半軸作無滑動的連續翻轉,每次翻轉60°,
∴每6次翻轉為一個循環組,
∵2018÷6=336余2,
∴經過2016次翻轉為第336個循環,點B在初始狀態時的位置,
而第2017次翻轉之后,點B的位置不變,仍在x軸上,
∵A(﹣2,0),
∴AB=2,
∴點B離原點的距離=2×2016=4032,
∴經過2017次翻轉之后,點B的坐標是(4032,0),
經過2018次翻轉之后,點B在B′位置,則△BB′C為等邊三角形,
此時BN=NC=1,B′N=![]() ,
,
故經過2018次翻轉之后,點B的坐標是:(4033,![]() ).
).
故答案為:(4033,![]() ).
).


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:初中數學 來源: 題型:
【題目】如圖![]() ,以
,以![]() 邊
邊![]() 和
和![]() 為邊作等邊
為邊作等邊![]() 和
和![]() ,連接
,連接![]() ,
,![]() ,
,
![]() 判斷
判斷![]() 與
與![]() 的數量關系,并求
的數量關系,并求![]() 與
與![]() 的夾角
的夾角![]() 的度數;
的度數;
![]() 繼續探索,如圖
繼續探索,如圖![]() ,以
,以![]() 的
的![]() 和
和![]() 為邊作正方形
為邊作正方形![]() 和
和![]() ,連接
,連接![]() 、
、![]() ,判斷
,判斷![]() 和
和![]() 的數量關系,并求出此時
的數量關系,并求出此時![]() 與
與![]() 的夾角;
的夾角;
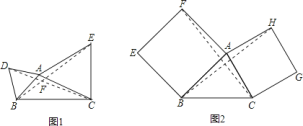
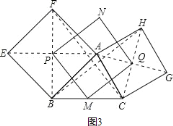
![]() 如圖
如圖![]() 中
中![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 、
、![]() 分別是正方形的中心,順次連接
分別是正方形的中心,順次連接![]() ,判斷四邊形
,判斷四邊形![]() 的形狀并證明.
的形狀并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若關于x的一元二次方程kx2-4x+2=0有實數根.
(1)求k的取值范圍;
(2)若ABC中,AB=AC=2,AB、BC的長是方程kx2-4x+2=0的兩根,求BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】基本圖形:在Rt△![]() 中,
中,![]() ,
,![]() 為
為![]() 邊上一點(不與點
邊上一點(不與點![]() ,
,![]() 重合),將線段
重合),將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() .
.
探索:(1)連接![]() ,如圖①,試探索線段
,如圖①,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;
(2)連接![]() ,如圖②,試探索線段
,如圖②,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;

聯想:(3)如圖③,在四邊形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,則
,則![]() 的長為 .
的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,AD=8cm,BC=12cm,M是BC上一點,且BM=9cm,點E從點A出發以1cm/s的速度向點D運動,點F從點C出發,以3cm/s的速度向點B運動,當其中一點到達終點,另一點也隨之停止,設運動時間為t,則當以A、M、E、F為頂點的四邊形是平行四邊形時,t=__________.
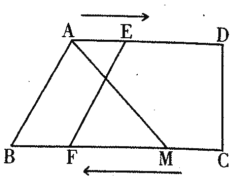
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC、BD相交于點O,CE∥BD,DE∥AC,若AC=4,則四邊形OCED的周長為( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某地有一座圓弧形的拱橋,橋下水面寬為8米(即AB=8米),拱頂高出水面為2米(即CD=2米).
(1)求這座拱橋所在圓的半徑.
(2)現有一艘寬6米,船艙頂部為正方形并高出水面1.5米的貨船要經過這里,此時貨船能順利通過這座拱橋嗎?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com