
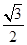 ,求證:△ABC是“好玩三角形”;
,求證:△ABC是“好玩三角形”;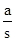 的值;
的值;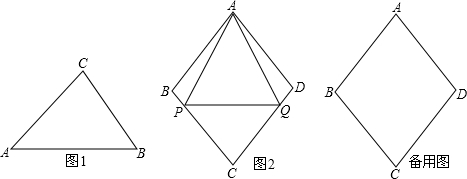
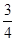 ②
②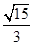 <tanβ<2
<tanβ<2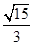 時,使得△APQ成為“好玩三角形”的個數為2.
時,使得△APQ成為“好玩三角形”的個數為2.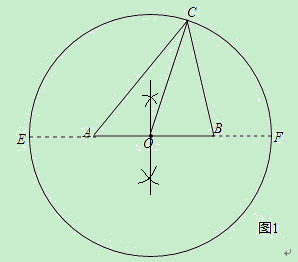

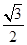 ,
,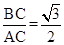
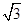 x,則AC=2x,
x,則AC=2x,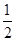 AC=x
AC=x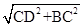 =
= 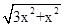 =2x,
=2x,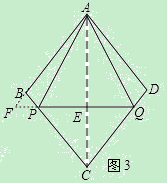
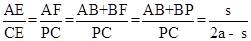 .
.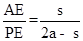 .
.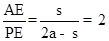 ,
,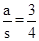 ,
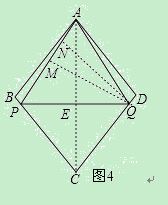
,
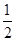 MP.
MP.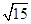 MN,
MN,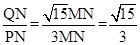 ,
,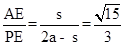 ,
,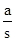 =
= 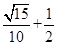
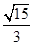 <tanβ<2時,有且只有一個△APQ能成為“好玩三角形”.
<tanβ<2時,有且只有一個△APQ能成為“好玩三角形”.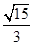 時,使得△APQ成為“好玩三角形”的個數為2.
時,使得△APQ成為“好玩三角形”的個數為2.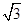 x,根據條件可以求出AC=2x,由三角函數可以求出BD=2x,從而得出AC=BD,從而得出結論;
x,根據條件可以求出AC=2x,由三角函數可以求出BD=2x,從而得出AC=BD,從而得出結論;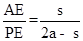 ,再分情況討論,當AE=PQ和AP=QM時,求出
,再分情況討論,當AE=PQ和AP=QM時,求出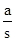 的值;
的值;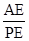 的值可以求出tanβ的取值范圍;
的值可以求出tanβ的取值范圍;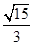 時,使得△APQ成為‘好玩三角形’的個數為2”是真命題.
時,使得△APQ成為‘好玩三角形’的個數為2”是真命題.

科目:初中數學 來源:不詳 題型:解答題
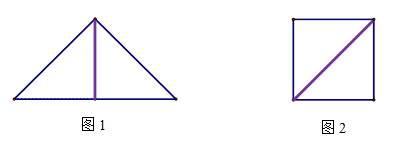
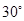 ,恰好可以拼成另一個含有30°角的直角三角形,那么在原來的兩個三角形紙片中,較大的與較小的紙片的相似比為________,請畫出拼接的示意圖;
,恰好可以拼成另一個含有30°角的直角三角形,那么在原來的兩個三角形紙片中,較大的與較小的紙片的相似比為________,請畫出拼接的示意圖;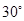 的直角三角形紙片拼成,請你畫出兩種不同拼法的示意圖.在拼成這個矩形的三角形中,若每種拼法中最小的三角形的斜邊長為
的直角三角形紙片拼成,請你畫出兩種不同拼法的示意圖.在拼成這個矩形的三角形中,若每種拼法中最小的三角形的斜邊長為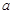 ,請直接寫出每種拼法中最大三角形的斜邊長.
,請直接寫出每種拼法中最大三角形的斜邊長.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
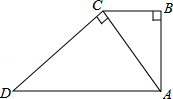
| A.2:3 | B.2:5 | C.4:9 | D.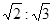 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
 CE時,EP+BP=__________.
CE時,EP+BP=__________.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
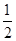 AB,點E、F分別為AB、AD的中點,則△AEF與多邊形BCDFE的面積之比為 ( )
AB,點E、F分別為AB、AD的中點,則△AEF與多邊形BCDFE的面積之比為 ( )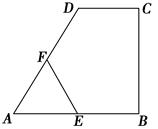
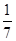 B.
B.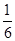 C.
C.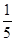 D.
D.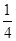
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
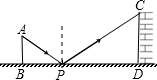
| A.6米 | B.8米 | C.18米 | D.24米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com