
【題目】如圖,AE是半圓O的直徑,弦AB=BC=2 ![]() ,弦CD=DE=2,連結OB,OD,求圖中兩個陰影部分的面積和.
,弦CD=DE=2,連結OB,OD,求圖中兩個陰影部分的面積和. 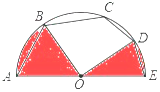
【答案】解:∵弦AB=BC,弦CD=DE, ∴點B是弧AC的中點,點D是弧CE的中點,
∴∠BOD=90°,
過點O作OF⊥BC于點F,OG⊥CD于點G.
則BF=FC= ![]() ,CG=GD=1,∠FOG=45°,
,CG=GD=1,∠FOG=45°,
在四邊形OFCG中,∠FCD=135°,
過點C作CN∥OF,交OG于點N,
則∠FCN=90°,∠NCG=135°﹣90°=45°,
∴△CNG為等腰三角形,
∴CG=NG=1,
過點N作NM⊥OF于點M,則MN=FC= ![]() ,
,
在等腰三角形MNO中,NO= ![]() MN=2,
MN=2,
∴OG=ON+NG=3,
在Rt△OGD中,OD= ![]() =
= ![]() =
= ![]() ,
,
即圓O的半徑為 ![]() ,
,
故S陰影=S扇形OBD= 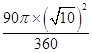 =
= ![]() π.
π.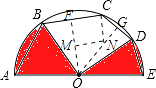
【解析】根據弦AB=BC,弦CD=DE,可得∠BOD=90°,∠BOD=90°,過點O作OF⊥BC于點F,OG⊥CD于點G,在四邊形OFCG中可得∠FCD=135°,過點C作CN∥OF,交OG于點N,判斷△CNG、△OMN為等腰直角三角形,分別求出NG、ON,繼而得出OG,在Rt△OGD中求出OD,即得圓O的半徑,代入扇形面積公式求解即可.
【考點精析】本題主要考查了扇形面積計算公式的相關知識點,需要掌握在圓上,由兩條半徑和一段弧圍成的圖形叫做扇形;扇形面積S=π(R2-r2)才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】定義:我們把對角線相等的四邊形叫做和美四邊形.
![]() 請舉出一種你所學過的特殊四邊形中是和美四邊形的例子.
請舉出一種你所學過的特殊四邊形中是和美四邊形的例子.
![]() 如圖1,E,F,G,H分別是四邊形ABCD的邊AB,BC,CD,DA的中點,已知四邊形EFGH是菱形,求證:四邊形ABCD是和美四邊形;
如圖1,E,F,G,H分別是四邊形ABCD的邊AB,BC,CD,DA的中點,已知四邊形EFGH是菱形,求證:四邊形ABCD是和美四邊形;
![]() 如圖2,四邊形ABCD是和美四邊形,對角線AC,BD相交于O,
如圖2,四邊形ABCD是和美四邊形,對角線AC,BD相交于O,![]() ,E、F分別是AD、BC的中點,請探索EF與AC之間的數量關系,并證明你的結論.
,E、F分別是AD、BC的中點,請探索EF與AC之間的數量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有A、B、C、D四個整數點(即各點均表示整數),且2AB=BC=3CD,若A、D兩點表示的數分別為﹣5和6,且AC的中點為E,BD的中點為M,BC之間距點B的距離為![]() BC的點N,則該數軸的原點為( )
BC的點N,則該數軸的原點為( )
![]()
A. 點E B. 點F C. 點M D. 點N
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,線段AC=6cm,線段BC=15cm,點M是AC的中點,在CB上取一點N,使得CN:NB=1:2,求MN的長.
(2)如圖2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
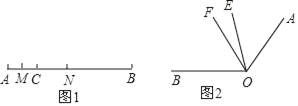
查看答案和解析>>
科目:初中數學 來源: 題型:
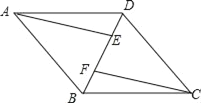
【題目】已知:如圖,四邊形ABCD是平行四邊形,AE∥CF,且分別交對角線BD于點E,F.
(1)求證:△AEB≌△CFD;
(2)連接AF,CE,若∠AFE=∠CFE,求證:四邊形AFCE是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“城市發展,交通先行”,我市啟動了緩堵保暢的高架橋快速通道建設工程,建成后將大大提升道路的通行能力.研究表明,某種情況下,高架橋上的車流速度V(單位:千米/時)是車流密度x(單位:輛/千米)的函數,且當0<x≤28時,V=80;當28<x≤188時,V是x的一次函數.函數關系如圖所示.
(1)求當28<x≤188時,V關于x的函數表達式;
(2)請你直接寫出車流量P和車流密度x之間的函數表達式;當x為多少時,車流量P(單位:輛/時)達到最大,最大值是多少?
(注:車流量是單位時間內通過觀測點的車輛數,計算公式為:車流量=車流速度×車流密度)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y= ![]() 的圖象位于第二、第四象限,那么關于x的一元二次方程x2+2x+k=0的根的情況是( )
的圖象位于第二、第四象限,那么關于x的一元二次方程x2+2x+k=0的根的情況是( )
A.方程有兩個不想等的實數根
B.方程不一定有實數根
C.方程有兩個相等的實數根
D.方程沒有實數根
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀對人成長的影響是巨大的,一本好書往往能改變人的一生,每年的4月23日被聯合國教科文組織確定為“世界讀書日”某校本學年開展了讀書活動,在這次活動中,八年級![]() 班40名學生讀書冊數的情況如表
班40名學生讀書冊數的情況如表
讀書冊數 | 4 | 5 | 6 | 7 | 8 |
人數 | 6 | 4 | 10 | 12 | 8 |
根據表中的數據,求:
(1)該班學生讀書冊數的平均數;
(2)該班學生讀書冊數的中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的長為2 ![]() cm,對角線交于點O,以AB,AO為鄰邊做平行四邊形AOCB,對角線交于點O,以AB、AO1為鄰邊做平行四邊形AO1C1B,…,依此類推,則平行四邊形AO6C6B的面積為cm2 .
cm,對角線交于點O,以AB,AO為鄰邊做平行四邊形AOCB,對角線交于點O,以AB、AO1為鄰邊做平行四邊形AO1C1B,…,依此類推,則平行四邊形AO6C6B的面積為cm2 . 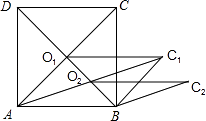
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com