
【題目】在平行四邊形![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,且
上,且![]() .
.
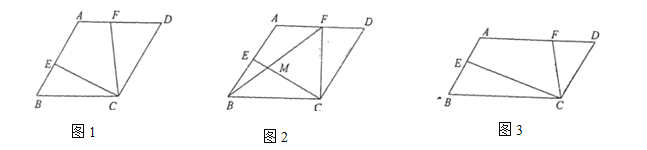
(1)如圖1,若![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,且點
,且點![]() 為
為![]() 的中點,連接
的中點,連接![]() 交
交![]() 于點
于點![]() ,求
,求![]() ;
;
(3)如圖3,若![]() ,探究線段
,探究線段![]() 、
、![]() 、
、![]() 三之間的數量關系,說明理由.
三之間的數量關系,說明理由.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)連接AC,根據題意判定平行四邊形ABCD為菱形,△ABC為等邊三角形,然后利用AAS定理判定△BCE≌△ACF,從而得出BE=AF,使問題得解;
(2)連接AC,過點M作MN⊥CF,由含30°直角三角形的性質求得![]() ,
,![]() ,設CN=x,則
,設CN=x,則![]() ,然后利用平行判定△FMN∽△FBC,根據相似三角形的性質求得
,然后利用平行判定△FMN∽△FBC,根據相似三角形的性質求得![]() ,然后利用勾股定理求解即可;
,然后利用勾股定理求解即可;
(3)連接AC,過點A作AK⊥BC,在DA上截取DH=CD,根據有一個角是60°的等腰三角形是等邊三角形判定△HCD是等邊三角形,然后根據AA定理判定△BCE ∽△FCH,根據相似三角形的性質求得![]() ,即HF=kBE,從而使問題得解.
,即HF=kBE,從而使問題得解.
解:(1)連接AC
因為在平行四邊形ABCD中,![]() ,
,![]()
∴平行四邊形ABCD為菱形,△ABC為等邊三角形
∴AC=BC,∠B=∠BAC=∠DAC=∠ACB=60°,
又∵![]()
∴∠ACE+∠BCE=∠ACE+∠ACF
∴∠BCE=∠ACF
∴△BCE≌△ACF
∴BE=AF
∴AB=AE+BE=![]()
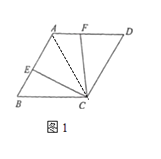
(2)連接AC,過點M作MN⊥CF
由(1)已證,△ABC為等邊三角形,△BCE≌△ACF
∵![]() 為
為![]() 的中點
的中點
∴CE⊥AB
∴在Rt△BCE中,∠BCE=30°
∴![]() ,
,![]()
由題意![]() ,∴∠BCF=90°
,∴∠BCF=90°
在Rt△AMCN中,∠CMN=30°
設CN=x,則![]()
∵MN⊥CF
∴MN∥BC
∴△FMN∽△FBC
∴![]() ,
,![]()
解得:![]()
∴![]()
在Rt△FMN中,![]()
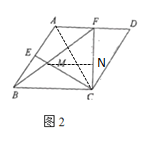
(3)由題意可知,在平行四邊形ABCD中,∠B=∠D=60°,![]()
連接AC,過點A作AK⊥BC,在DA上截取DH=CD
∵DH=CD,∠B=∠D=60°
∴△HCD是等邊三角形
∴∠HCD=60°
又∵∠ECF=60°
∴∠BCE+∠ECH=∠FCH+∠ECH
∴∠BCE =∠FCH
∴△BCE ∽△FCH
∴![]() ,即HF=kBE
,即HF=kBE
∴CD=DF+HF=DF+ kBE
又∵![]()
∴![]()


 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:初中數學 來源: 題型:
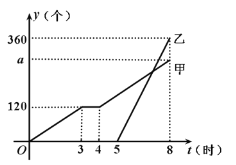
【題目】某天,甲車間工人加工零件,工作中有一次停產檢修機器,然后以原來的工作效率繼續加工,由于任務緊急,乙車間加入與甲車間一起生產零件,兩車間各自加工零件的數量y(個)與甲車間加工時間t(時)之間的函數圖象如圖所示.
(1)求乙車間加工零件的數量y與甲車間加工時間t之間的函數關系式,并寫出t的取值范圍.
(2)求甲車間加工零件總量a.
(3)當甲、乙兩車間加工零件總數量為320個時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請僅用無刻度的直尺完成下列畫圖,不寫畫法,保留畫圖痕跡.(用虛線表示畫圖過程,實線表示畫圖結果)
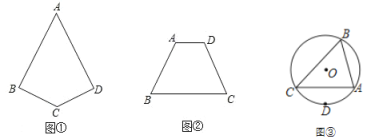
(1)如圖①,四邊形 ABCD 中,AB=AD,∠B=∠D,畫出四邊形 ABCD 的對稱軸 m;
(2)如圖②,四邊形 ABCD 中,AD∥BC,∠A=∠D,畫出 BC 邊的垂直平分線 n.
(3)如圖③,△ABC 的外接圓的圓心是點 O,D 是![]() 的中點,畫一條直線把△ABC 分成面積相等的兩部分.
的中點,畫一條直線把△ABC 分成面積相等的兩部分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在菱形ABCD中,AB=4,∠BAD=120°,點P是直線AB上任意一點,聯結PC,在∠PCD內部作射線CQ與對角線BD交于點Q(與B、D不重合),且∠PCQ=30°.
(1)如圖,當點P在邊AB上時,如果BP=3,求線段PC的長;
(2)當點P在射線BA上時,設![]() ,求y關于
,求y關于![]() 的函數解析式及定義域;
的函數解析式及定義域;
(3)聯結PQ,直線PQ與直線BC交于點E,如果![]() 與
與![]() 相似,求線段BP的長.
相似,求線段BP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B在反比例函數![]() 的圖象上,點C,D在反比例函數
的圖象上,點C,D在反比例函數![]() 的圖象上,AC//BD//y軸,已知點A,B的橫坐標分別為1,2,△OAC與△ABD的面積之和為
的圖象上,AC//BD//y軸,已知點A,B的橫坐標分別為1,2,△OAC與△ABD的面積之和為![]() ,則k的值為( )
,則k的值為( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 的圖象經過坐標原點
的圖象經過坐標原點![]() ,且與
,且與![]() 軸另交點為
軸另交點為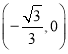 .
.
(1)求拋物線![]() 的解析式;
的解析式;
(2)如圖![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 相交于點
相交于點![]() 和點
和點![]() (點
(點![]() 在第二象限),求
在第二象限),求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
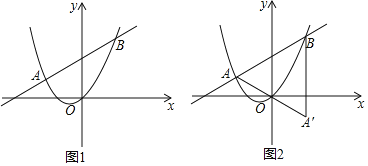
(3)在(2)中,若![]() ,設點
,設點![]() 是點
是點![]() 關于原點
關于原點![]() 的對稱點,如圖
的對稱點,如圖![]() .平面內是否存在點
.平面內是否存在點![]() ,使得以點
,使得以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,直接寫出點
為頂點的四邊形是菱形?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,分別過點![]() ,
,![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 和
和![]() ,探究直線
,探究直線![]() 、
、![]() 與函數
與函數![]() 的圖象(雙曲線)之間的關系,下列結論正確的是( )
的圖象(雙曲線)之間的關系,下列結論正確的是( )
A.兩條直線可能都不與雙曲線相交
B.當![]() 時,兩條直線與雙曲線的交點到原點的距離不相等
時,兩條直線與雙曲線的交點到原點的距離不相等
C.當![]() 時,兩條直線與雙曲線的交點都在
時,兩條直線與雙曲線的交點都在![]() 軸左側
軸左側
D.當![]() 時,兩條直線與雙曲線的交點都在
時,兩條直線與雙曲線的交點都在![]() 軸右側
軸右側
查看答案和解析>>
科目:初中數學 來源: 題型:
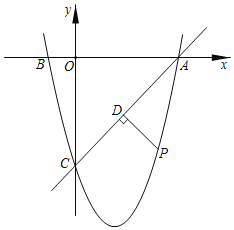
【題目】如圖,在平面直角坐標系中,已知點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,拋物線
,拋物線![]() 圖象經過
圖象經過![]() 三點.
三點.
(1)求![]() 兩點的坐標;
兩點的坐標;
(2)求拋物線的解析式;
(3)若點![]() 是直線
是直線![]() 下方的拋物線上的一個動點,作
下方的拋物線上的一個動點,作![]() 于點
于點![]() ,當
,當![]() 的值最大時,求此時點
的值最大時,求此時點![]() 的坐標及
的坐標及![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com