
【題目】二次函數y=ax2+bx+c(a<0)的圖象與x軸的兩個交點A、B的橫坐標分別為﹣3、1,與y軸交于點C,下面四個結論:
①16a+4b+c>0:
②若P(﹣5,y1),Q(![]() ,y2)是函數圖象上的兩點,則y1<y2;
,y2)是函數圖象上的兩點,則y1<y2;
③c=3a;
④若△ABC是等腰三角形,則b=﹣![]() 或﹣
或﹣![]() .
.
其中正確的有_____.(請將正確結論的序號全部填在橫線上)
【答案】①④.
【解析】
①根據拋物線開口方向和與x軸的兩交點可知:當x=-4時,y<0,即16a-4b+c<0;②根據圖象與x軸的交點A、B的橫坐標分別為-3,1確定對稱軸是:x=-1,可得:(﹣4.5,y3)與Q(![]() ,y2)是對稱點,所以y1<y2;③根據對稱軸和x=1時,y=0可得結論;④要使△ACB為等腰三角形,則必須保證AB=BC=4或AB=AC=4或AC=BC,先計算c的值,再聯立方程組可得結論.
,y2)是對稱點,所以y1<y2;③根據對稱軸和x=1時,y=0可得結論;④要使△ACB為等腰三角形,則必須保證AB=BC=4或AB=AC=4或AC=BC,先計算c的值,再聯立方程組可得結論.
解:①∵a<0,
∴拋物線開口向下,
∵圖象與x軸的交點A、B的橫坐標分別為﹣3,1,
∴當x=﹣4時,y<0,
即16a﹣4b+c<0;
故①正確,符合題意;
②∵圖象與x軸的交點A、B的橫坐標分別為﹣3,1,
∴拋物線的對稱軸是:x=﹣1,
∵P(﹣5,y1),Q(![]() ,y2),
,y2),
﹣1﹣(﹣5)=4,![]() ﹣(﹣1)=3.5,
﹣(﹣1)=3.5,
由對稱性得:(﹣4.5,y3)與Q(![]() ,y2)是對稱點,
,y2)是對稱點,
∴則y1<y2;
故②不正確,不符合題意;
③∵﹣![]() =﹣1,
=﹣1,
∴b=2a,
當x=1時,y=0,即a+b+c=0,
∴3a+c=0,
∴c=﹣3a,
故③錯誤,不符合題意;
④要使△ACB為等腰三角形,則必須保證AB=BC=4或AB=AC=4或AC=BC,
當AB=BC=4時,
∵BO=1,△BOC為直角三角形,
又∵OC的長即為|c|,
∴c2=16﹣1=15,
∵由拋物線與y軸的交點在y軸的正半軸上,
∴c=![]() ,
,
與b=2a、a+b+c=0聯立組成解方程組,解得b=﹣![]() ;
;
同理當AB=AC=4時,
∵AO=3,△AOC為直角三角形,
又∵OC的長即為|c|,
∴c2=16﹣9=7,
∵由拋物線與y軸的交點在y軸的正半軸上,
∴c=![]() ,
,
與b=2a、a+b+c=0聯立組成解方程組,解得b=﹣![]() ;
;
同理當AC=BC時,
在△AOC中,AC2=9+c2,
在△BOC中,BC2=c2+1,
∵AC=BC,
∴1+c2=c2+9,此方程無實數解.
經解方程組可知有兩個b值滿足條件.
故④正確,符合題意.
綜上所述,正確的結論是①④.
故答案是:①④.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
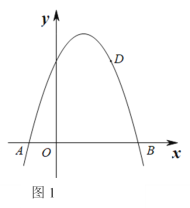
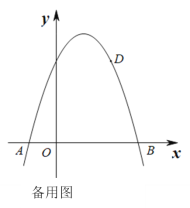
【題目】如圖1,拋物線y=ax2+bx +3與x軸的交點為A和B,其中點A(-1,0),且點D(2,3)在該拋物線上.
(1)求該拋物線所對應的函數解析式;
(2)點P是線段AB上的動點(點P不與點A,B重合),過點P作PQ⊥x軸交該拋物線于點Q,連接AQ,DQ,記點P的橫坐標為t.
①若![]() 時,求△
時,求△![]() 面積的最大值;
面積的最大值;
②若△![]() 是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
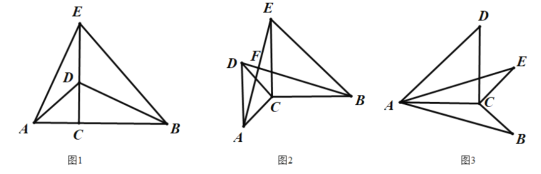
【題目】(1)問題發現:如圖1,已知點![]() 為線段
為線段![]() 上一點,分別以線段
上一點,分別以線段![]() 為直角邊作兩個等腰直角三角形,
為直角邊作兩個等腰直角三角形,![]() ,連接
,連接![]() ,線段
,線段![]() 之間的數量關系為__;位置關系為_________.
之間的數量關系為__;位置關系為_________.
(2)拓展研究:如圖2,把![]() 繞點C逆時針旋轉,線段
繞點C逆時針旋轉,線段![]() 交于點F,則
交于點F,則![]() 之間的關系是否仍然成立,說明理由;
之間的關系是否仍然成立,說明理由;
(3)解決問題:如圖3,已知![]() ,連接
,連接![]() ,把線段AB繞點A旋轉,若
,把線段AB繞點A旋轉,若![]() ,請直接寫出線段
,請直接寫出線段![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個袋中均有三張除所標數值外完全相同的卡片,甲袋中的三張卡片上所標的數值分別為﹣7,﹣1,3,乙袋中的三張卡片上所標的數值分別為﹣2,1,6.先從甲袋中隨機取出一張卡片,用x表示取出的卡片上標的數值,再從乙袋中隨機取出一張卡片,用y表示取出的卡片上標的數值,把x、y分別作為點A的橫坐標、縱坐標.
(1)用適當的方法寫出點A(x,y)的所有情況;
(2)求點A落在第二象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了豐富學生課余生活,開展了“第二課堂”活動,推出了以下四種選修課程:![]() .繪畫;
.繪畫;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演講;
.演講;![]() .書法.學校規定:每個學生都必須報名且只能選擇其中的一個課程.學校隨機抽查了部分學生,對他們選擇的課程情況進行了統計,并繪制了如下兩幅不完整的統計圖.
.書法.學校規定:每個學生都必須報名且只能選擇其中的一個課程.學校隨機抽查了部分學生,對他們選擇的課程情況進行了統計,并繪制了如下兩幅不完整的統計圖.
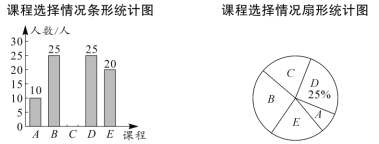
請結合統計圖中的信息解決下列問題:
(1)這次抽查的學生人數是多少人?
(2)將條形統計圖補充完整.
(3)求扇形統計圖中課程![]() 所對應扇形的圓心角的度數.
所對應扇形的圓心角的度數.
(4)如果該校共有1200名學生,請你估計該校選擇課程![]() 的學生約有多少人.
的學生約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx(a>0)過點E(8,0),矩形ABCD的邊AB在線段OE上(點A在點B的左側),點C、D在拋物線上,∠BAD的平分線AM交BC于點M,點N是CD的中點,已知OA=2,且OA:AD=1:3.
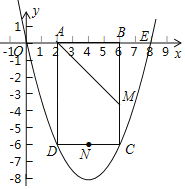
(1)求拋物線的解析式;
(2)F、G分別為x軸,y軸上的動點,順次連接M、N、G、F構成四邊形MNGF,求四邊形MNGF周長的最小值;
(3)在x軸下方且在拋物線上是否存在點P,使△ODP中OD邊上的高為![]() ?若存在,求出點P的坐標;若不存在,請說明理由;
?若存在,求出點P的坐標;若不存在,請說明理由;
(4)矩形ABCD不動,將拋物線向右平移,當平移后的拋物線與矩形的邊有兩個交點K、L,且直線KL平分矩形的面積時,求拋物線平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
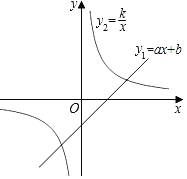
【題目】如圖,已知一次函數y1=ax+b(a≠0)與反比例函數y2=![]() (k>0),兩函數圖象交于(4,1),(﹣2,n)兩點.
(k>0),兩函數圖象交于(4,1),(﹣2,n)兩點.
(1)求a,k的值;
(2)若y2>y1>0,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
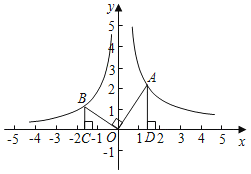
【題目】如圖,第一象限內的點A在反比例函數y=![]() 上,第二象限的點B在反比例函數y=
上,第二象限的點B在反比例函數y=![]() 上,且OA⊥OB,
上,且OA⊥OB,![]() ,BC、AD垂直于x軸于C、D,則k的值為_____.
,BC、AD垂直于x軸于C、D,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是△ABC的邊AB上一點,CE∥AB,DE交AC于點F,若FA=FC.
(1)求證:四邊形ADCE是平行四邊形;
(2)若AE⊥EC,EF=EC=5,求四邊形ADCE的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com