
【題目】在一次聚會上,規定每兩個人見面必須握手,且握手1次.
(1)若參加聚會的人數為3,則共握手 次;若參加聚會的人數為5,則共握手 次;
(2)若參加聚會的人數為n(n為正整數),則共握手 次;
(3)若參加聚會的人共握手28次,請求出參加聚會的人數.
(4)嘉嘉由握手問題想到了一個數學問題:若線段AB上共有m個點(不含端點A,B),線段總數為多少呢?請直接寫出結論.
【答案】(1)3;10;(2)![]() ;(3)參加聚會的人數為8人;(4)
;(3)參加聚會的人數為8人;(4)![]() .
.
【解析】
(1)(2)(3)根據題意每個人要與他自己以外的人握手一次,當兩人只握手一次,所以握手次數為:![]() ×聚會人數×(聚會人數-1),故可進行計算求解;(4)由線段上AB上共有m個點(不含端點A,B),則相當于聚會人數為m+2,則根據公式即可寫出線段數.
×聚會人數×(聚會人數-1),故可進行計算求解;(4)由線段上AB上共有m個點(不含端點A,B),則相當于聚會人數為m+2,則根據公式即可寫出線段數.
(1)若參加聚會的人數為3,則共握手3次;
若參加聚會的人數為5,則共握手10次;
(2)若參加聚會的人數為n(n為正整數),則共握手![]() 次
次
(3)由題意得:![]() =28,即
=28,即![]()
解得,![]() ,
,![]() (舍去)
(舍去)
答:參加聚會的人數為8人.
(4)由線段上AB上共有m個點(不含端點A,B),則相當于聚會人數為m+2,則根據公式即可寫出線段數為![]()


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:初中數學 來源: 題型:
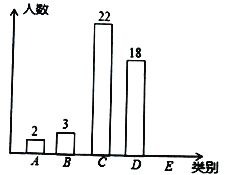
【題目】某班為了解學生每周進行體育鍛煉的時間情況,對全班![]() 名學生進行調查,按每周進行體育鍛煉的時間
名學生進行調查,按每周進行體育鍛煉的時間![]() (單位:小時),將學生分成五類:
(單位:小時),將學生分成五類:![]() 類
類![]() ,
,![]() 類
類![]() ,
,![]() 類
類![]() ,
,![]() 類
類![]() ,
,![]() 類
類![]() .繪制成尚不完整的條形統計圖如圖. 根據以上信息,解答下列問題:
.繪制成尚不完整的條形統計圖如圖. 根據以上信息,解答下列問題:
(1)![]() 類學生有 人,補全條形統計圖;
類學生有 人,補全條形統計圖;
(2)![]() 類學生人數占被調查總人數的 %;
類學生人數占被調查總人數的 %;
(3)從該班每周進行體育鍛煉時間在![]() 的學生中任選人
的學生中任選人![]() 人,求這
人,求這![]() 人每周進行體育鍛煉時間都在
人每周進行體育鍛煉時間都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
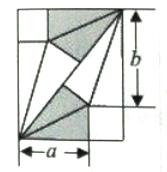
【題目】我國古代數學家劉徽將勾股形(古人稱直角三角形為勾股形)分割成一個正方形和兩對全等的直角三角形,得到一個恒等式,后人借助這種分割方法所得的圖形證明了勾股定理,如圖所示的長方形由兩個這樣的圖形拼成,若![]() ,
,![]() ,則該長方形的面積為__________.
,則該長方形的面積為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四位同學在研究函數y=x2+bx+c(b,c是常數)時,甲發現當x=1時,函數有最小值;乙發現﹣1是方程x2+bx+c=0的一個根;丙發現函數的最小值為3;丁發現當x=2時,y=4,已知這四位同學中只有一位發現的結論是錯誤的,則該同學是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=4,BC=3,點D是AC的中點,連接BD,按以下步驟作圖:①分別以B,D為圓心,大于![]() BD的長為半徑作弧,兩弧相交于點P和點Q;②作直線PQ交AB于點E,交BC于點F,則BF=( )
BD的長為半徑作弧,兩弧相交于點P和點Q;②作直線PQ交AB于點E,交BC于點F,則BF=( )
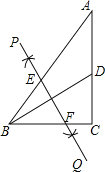
A. ![]() B. 1C.
B. 1C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
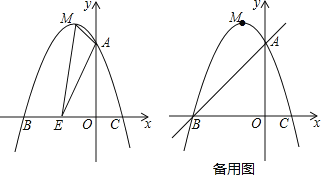
【題目】如圖,拋物線y=ax2+bx+3交y軸于點A,交x軸于點B(-3,0)和點C(1,0),頂點為點M.
(1)求拋物線的解析式;
(2)如圖,點E為x軸上一動點,若△AME的周長最小,請求出點E的坐標;
(3)點F為直線AB上一個動點,點P為拋物線上一個動點,若△BFP為等腰直角三角形,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場試銷一種成本為![]() 元/件的T 恤,規定試銷期間單價不低于成本單價,又獲利不得高于
元/件的T 恤,規定試銷期間單價不低于成本單價,又獲利不得高于![]() ,經試銷發現,銷售量
,經試銷發現,銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元/件)符合一次函數
(元/件)符合一次函數![]() ,且
,且![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(1)寫出銷售單價![]() 的取值范圍;
的取值范圍;
(2)求出一次函數![]() 的解析式;
的解析式;
(3)若該商場獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式,銷售單價定為多少時,商場可獲得最大利潤,最大利潤是多少?
之間的關系式,銷售單價定為多少時,商場可獲得最大利潤,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數![]() ,如表是函數的幾組對應值:
,如表是函數的幾組對應值:
x |
|
|
|
|
|
| 0 | 1 | 2 | 3 |
| 4 |
|
y |
|
|
|
|
|
| 0 |
|
|
|
|
|
|
請你根據學習函數的經驗,利用表格所反映出的y與x之間的變化規律,對該函數的圖象與性質進行探究![]() 下面是小騰的探究過程,請補充完整.
下面是小騰的探究過程,請補充完整.
![]() 如圖所示,在平面直角坐標系xOy中,描出了上表中各對對應值為坐標的點
如圖所示,在平面直角坐標系xOy中,描出了上表中各對對應值為坐標的點![]() 根據描出的點,畫出該函數的圖象
根據描出的點,畫出該函數的圖象
![]() 根據函數圖象,按要求填空:
根據函數圖象,按要求填空:
![]() 在y軸左側該函數圖象有最______點,其坐標為______.
在y軸左側該函數圖象有最______點,其坐標為______.
![]() 當
當![]() 時,該函數y隨x的增大而______.
時,該函數y隨x的增大而______.
![]() 當方程
當方程![]() 只有一個解時,則a的取值范圍為______.
只有一個解時,則a的取值范圍為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com