
【題目】如圖,AB=AC,BE與CF是△ABC的高線,且BE與CF相交于點H.
(1)求證:HB=HC;
(2)不添加輔助線,直接寫出圖中所有的全等三角形.
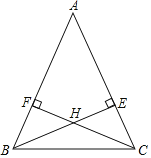
【答案】(1)證明見解析;(2)全等三角形有△AEB≌△AFC,△BEC≌△CFB,△BFH≌△CEH.
【解析】
(1)根據高求出∠BEC=∠BFC=90°,根據等腰三角形的性質得出∠ABC=∠ACB,根據三角形內角和定理求∠EBC=∠BCF,根據等腰三角形的判定得出即可;
(2)根據全等三角形的判定逐個判斷即可.
解:(1)∵BE與CF是△ABC的高線,
∴∠BEC=∠BFC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BEC+∠ACB+∠EBC=180°,∠CFB+∠ABC+∠BCF=180°,
∴∠EBC=∠BCF,
∴HB=HC;
(2)解:由(1)可知:AB=AC, ∠BEC=∠BFC=90°, ∠ABC=∠ACB,∠EBC=∠BCF
∴利用ASA定理可以判定△AEB≌△AFC;
利用AAS定理可以判定△BEC≌△CFB;△BFH≌△CEH,
∴全等三角形有△AEB≌△AFC,△BEC≌△CFB,△BFH≌△CEH.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() ,
,![]() ,已知點
,已知點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 是該直線上的一個動點.
是該直線上的一個動點.
(1)![]() ________;
________;![]() 的坐標為__________;
的坐標為__________;
(2)若點![]() 在第二象限內運動,試寫出
在第二象限內運動,試寫出![]() 的面積
的面積![]() 關于
關于![]() 的函數解析式.
的函數解析式.
(3)探究:若點![]() 在該直線上任意運動,當
在該直線上任意運動,當![]() 的面積為6時,點
的面積為6時,點![]() 的坐標為________.
的坐標為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,E、F分別是DC和CB的延長線上的點,且DE=BF,連接AE、AF、EF.

(1)求證:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE繞旋轉中心 點,按順時針方向旋轉 度得到;
(3)若BC=8,DE=6,求△AEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
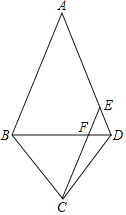
【題目】如圖,在四邊形ABCD中,AB=AD,BC=DC,點E為AD邊上一點,連接BD、CE,CE與BD交于點F,且CE∥AB,若AB=8,CE=6,若△FCD的面積為2![]() ,則四邊形ABCD的面積為_____.
,則四邊形ABCD的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
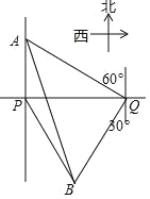
【題目】一輪船在P處測得燈塔A在正北方向,燈塔B在南偏東30°方向,輪船向正東航行了900m,到達Q處,測得A位于北偏西60°方向, B位于南偏西30°方向.
(1)線段BQ與PQ是否相等?請說明理由;
(2)求A、B間的距離(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
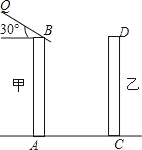
【題目】如圖,是住宅區內的兩幢樓,它們的高AB=CD=30m,兩樓間的距離AC=30m,現需了解甲樓對乙樓的采光的影響情況.
(1)當太陽光與水平線的夾角為30°角時,求甲樓的影子在乙樓上有多高(精確到0.1m,![]() =1.73);
=1.73);
(2)若要甲樓的影子剛好不落在乙樓的墻上,此時太陽與水平線的夾角為多少度?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com