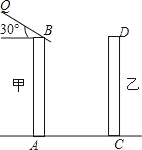
【題目】如圖，是住宅區內的兩幢樓，它們的高AB=CD=30m，兩樓間的距離AC=30m，現需了解甲樓對乙樓的采光的影響情況．
（1）當太陽光與水平線的夾角為30°角時，求甲樓的影子在乙樓上有多高（精確到0.1m，
=1.73）；
（2）若要甲樓的影子剛好不落在乙樓的墻上，此時太陽與水平線的夾角為多少度？
【答案】（1）12.7（2）當太陽光與水平線夾角為45°時，甲樓的影子剛好不落在乙樓的墻上
【解析】試題分析：（1）通過投影的知識結合題意構造直角三角形Rt△BEF，設BF=x，解此直角三角形可得x的值；由此可得EC的數值，即甲樓的影子在乙樓上有多高；
（2）要甲樓的影子剛好不落在乙樓的墻上，易得△ABC為等腰三角形，且AC=30m，容易求得當太陽光與水平線夾角為45°時，甲樓的影子剛好不落在乙樓的墻上．
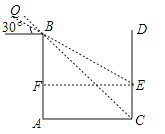
試題解析：解：（1）如圖，延長OB交DC于E，作EF⊥AB，交AB于F．在Rt△BEF中，∵EF=AC=30m，∠FEB=30°，∴BE=2BF．
設BF=x，則BE=2x．根據勾股定理知：BE2=BF2+EF2，∴（2x）2=x2+302，∴
（負值舍去），∴x≈17.3（m）．因此，EC=30﹣17.3=12.7（m）．
（2）當甲幢樓的影子剛好落在點C處時，△ABC為等腰三角形，因此，當太陽光與水平線夾角為45°時，甲樓的影子剛好不落在乙樓的墻上．
科目：初中數學 來源： 題型：
【題目】甲、乙兩家商場平時以同樣價格出售相同的商品，春節期間兩家商場都讓利酬賓，其中甲商場所有商品按8折出售，乙商場對一次購物中超過200元后的價格部分打7折．
（1）以x（單位：元）表示商品原價，y（單位：元）表示購物金額，分別就兩家商場的讓利方式寫出y關于x的函數解析式；
（2）在同一直角坐標系中畫出（1）中函數的圖象；
（3）春節期間如何選擇這兩家商場去購物更省錢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知數軸上點
表示的數為
，點
表示的數為
，點
到點，點的距離相等，動點
從點出發，以每秒
個單位長度的速度沿數軸向右勻速運動，設運動的時間為
（
）秒．
（1）點表示的數是 ．
（2）點表示的數是 ．（用含有的代數式表示）；
（3）求當等于多少秒時，點與點之間的距離為個單位長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
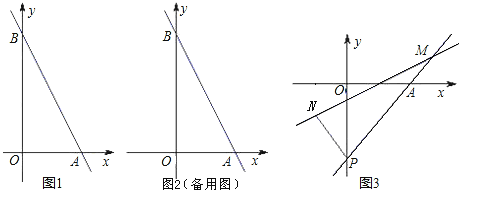
【題目】如圖1，在平面直角坐標系中，直線AB與x軸，y軸分別交于點A（2，0）, B（0，4）.
（1）求直線AB的解析式；
（2）若點M為直線y=mx在第一象限上一點，且△ABM是等腰直角三角形，求m的值．
（3）如圖3，過點A（2，0）的直線
交y軸負半軸于點P，N點的橫坐標為-1，過N點的直線
交AP于點M.求
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知A＝x－2y，B＝－x－4y＋1.
（1）求2(A＋B)－(A－B)；（結果用含x，y的代數式表示）
（2）當
與
互為相反數時，求(1)中代數式的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分線EF分別交AD、BC于點E、F，垂足為O．
（1）如圖1，連接AF、CE．求證四邊形AFCE為菱形，并求AF的長；
（2）如圖2，動點P、Q分別從A、C兩點同時出發，沿△AFB和△CDE各邊勻速運動一周．即點P自A→F→B→A停止，點Q自C→D→E→C停止．在運動過程中，
①已知點P的速度為每秒5cm，點Q的速度為每秒4cm，運動時間為t秒，當A、C、P、Q四點為頂點的四邊形是平行四邊形時，求t的值．
②若點P、Q的運動路程分別為a、b（單位：cm，ab≠0），已知A、C、P、Q四點為頂點的四邊形是平行四邊形，求a與b滿足的數量關系式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
